필요조건과 충분조건, statement와 expression

https://math.stackexchange.com/questions/2985999/draw-a-venn-diagram-showing-an-event-along-with-its-sufficient-and-necessary-con

 

 

헷갈릴 때 쯤 한번씩 되뇌어 주어야 한다.

 

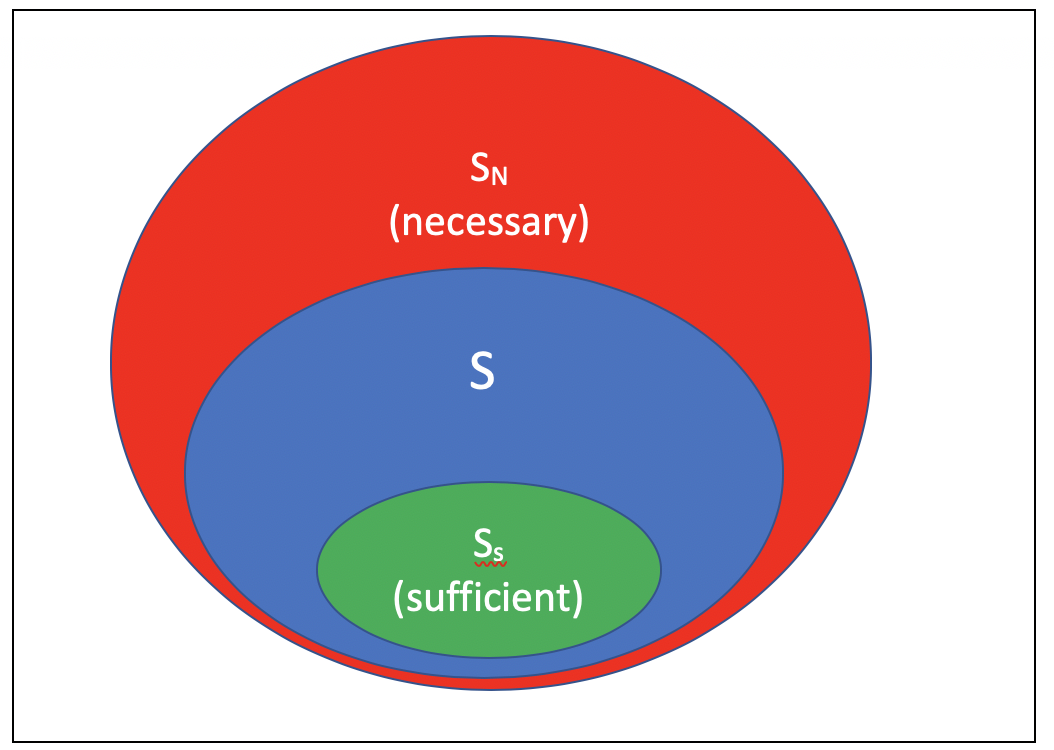
'A이면 B이다'라는 명제가 참일 때,

 

A는 B이기 위한 충분조건이다.

≡ A는 B를 만족시키기에 충분(sufficient)하다.

≡ A에서 조건을 조금 완화시켜도 여전히 B를 만족시킬지도 모른다.

≡ A이면 충분히 B라고 했지, A가 아니라고 해서 B가 아닌 것은 아니다.

 

B는 A이기 위한 필요조건이다.

≡ A를 만족하려면 우선 B를 만족시키는 것이 필요(necessary)하다.

≡ A를 만족시켜도 B를 만족시키려면 조건이 더 필요할지도 모른다.

≡ B를 만족시키지 않으면 A 만족 여부는 볼 필요가 없다.

 

무언가를 충분히 준비했다는 것은 조금 남는 정도로 준비했다는 말과 동치이다. 조금 빼도 된다는 말이다. 따라서 A에서 조건을 조금 완화시켜도 B가 만족될 가능성이 있다. 

 

무언가가 필요하다는 것은 거기서 조금이라도 빠지면 안 된다는 말과 동치이다. 오히려 더 필요할지도 모른다. 따라서 B를 만족하지 않으면 A는 자동으로 만족하지 않는다.

 

예를 들어 아래와 같은 명제가 있다.

 

β가 벡터공간 V의 기저라면 β의 원소들은 선형독립이다.

 

여기서 β의 원소들이 선형독립인 것은 β가 벡터공간의 기저이기 위한 필요조건이다. β의 원소들이 선형독립이 아니면 따져볼 것도 없다. β가 선형독립이라고 해서 기저가 되지는 않는다. 조건이 더 필요하다. β가 벡터공간의 기저인 것은 β의 원소들이 선형독립이기 위한 충분조건이다. 기저라면 정의에 의해 원소들이 선형독립이기 때문이다. 즉, 기저라는 사실은 선형독립이라는 성질을 주기에 충분하다. 다만 기저가 아니라고 해서 선형독립이 아닌 것은 아니다. 기저에서 원소를 몇 개 빼면 기저는 아니지만 여전히 선형독립이다.

 

한마디로, 충분조건은 다른 경우의 여지를 주며, 필요조건은 여지를 주지 않는다.

 

---

 

이걸 따져보기에 좋은 예시가 있다. 프로그래밍에서 statement는 어떤 동작을 발생시키는 코드를 말하고 expression은 값이 평가(evaluate)되는 코드를 말한다. 값이 평가되려면 당연히 동작이 발생해야 한다. 그래서 모든 expression은 statement이다. 하지만 statement이면서 expression이 아닌 것이 존재한다. 대표적으로 파이썬의 대입 명령문이다. import도 statement이지만 expression이 아니다.

 

이것을 위의 구조에 대입해보면,

 

코드 A가 expression인 것은 코드 A가 statement이기 위한 충분조건이다.

≡ 코드 A가 expression임을 아는 것은 코드 A가 statement임을 확인하기에 충분하다.

≡ 코드 A가 expression이 아니라고 해서 코드 A가 statement가 아닌 것은 아니다.

 

코드 A가 statement인 것은 코드 A가 expression이기 위한 필요조건이다.

≡ 코드 A가 expression이려면 우선 코드 A가 statement임이 필요하다.

≡ 코드 A가 statement가 아니라면 코드 A가 expression인지 아닌지는 볼 필요도 없다.

 

 

끗