테일러 급수의 수렴 조건

 

 

본 글의 내용 대부분은 교양을 위한 대학수학 1(김성기 외, 교우사)에서 가져왔습니다.

 

---

 

미분 가능한 함수 $f(x)$가 주어져있을 때, $x = 0$ 근방에서 $f(x)$와 "가장 가까운" 1차 함수는 접선이다.

 

$$p_1(x) = f(0) + f'(0) x$$

 

여기서 두 함수가 "가깝다"는 것은, 적어도 $x=0$ 근방에서는 $p_1(x)$로 $f(x)$를 잘 표현할 수 있다는 뜻이다. 혹은 $f(x)$ 대신 $p_1(x)$를 써도 어느 정도는 무방하다고 말할 수도 있을 것이다. 이것을 수학적으로는 두 함수의 차이를 이용해서 표현할 수 있다.

 

$$\lim_{x\to 0} \frac{f(x)-p_1(x)}{x} = \lim_{x\to 0} \frac{f(x)-f(0)}{x-0} - f'(0) = 0$$

 

즉, $f(x)$와 $p_1(x)$의 차이는 $x$보다 더 빨리 0에 수렴한다.

 

1차 함수보다 원래 함수에 더 가까운 다항식을 만들고 싶다면 차수를 높이면 된다. $x=0$에서 $f(x)$와 가장 가까운 2차 함수는 무엇일까? 즉, 아래를 만족하는 2차 함수 $p_2(x) := a_0 + a_1 x + a_2 x^2$를 알고 싶다.

 

$$
\lim_{x\to 0} \frac{f(x)-(a_0 + a_1 x + a_2 x^2)}{x^2} = 0
$$

 

이 식의 의미는, $f(x)$를 polynomial로 표현할 수 있다면 $f(x)-p_2(x)$에는 $x^2$ "성분"이 남지 않아야 한다는 뜻이다. 그래야 분자에 $x^3$ 이상의 성분만 남아서 분자가 분모보다 더 빨리 수렴하기 때문이다. 위 극한의 값이 존재하려면 분자가 0이어야 하므로

 

$$f(0) - a_0 = 0 \Rightarrow a_0 = f(0)$$

 

로피탈 정리를 적용하면

 

$$
\lim_{x\to 0} \frac{f'(x)- a_1 x - 2 a_2 x}{2x} = 0
$$

 

로부터 $a_1 = f'(0)$이다. 로피탈을 한번 더 적용하면

 

$$
\lim_{x\to 0} \frac{f''(x)- 2a_2 }{2} = 0
$$

 

로부터 $a_2 = f''(0)/2$이다. 따라서 $x=0$ 근방에서 미분가능한 함수 $f(x)$와 가장 가까운 2차 함수는

 

$$ p_2(x) = f(0) + f'(0)x + \frac{f''(0)}{2} x^2$$

 

이다.

 

이것을 $n$차 다항식으로 일반화하면, 미분가능한 함수 $f(x)$의 $x=0$ 근방에서 $f(x)$와 가장 가까운 $n$차 다항식 $p_n(x)$는 다음을 만족한다.

 

$$
\lim_{x\to 0} \frac{f(x)-p_n(x)}{x^n} = 0
$$

 

이 다항식 $p_n(x)$를 $f(x)$의 $n$차 근사다항식이라고 부르며, 아래와 같이 표기한다.

 

$$f(x) \sim p_n(x)$$

 

앞의 과정을 반복하면 $p_n(x)$가 아래와 같음을 알 수 있다.

 

\begin{align}
p_n(x) &= f(0) + f'(0)x + \frac{f''(0)}{2!}x^2 + ... + \frac{f^{(n)}(0)}{n!}x^n \\
&= \sum_{k=0}^{n} \frac{f^{(k)}(0)}{k!}x^k
\end{align}

 

즉, $x=0$에서의 정보만을 이용해서 $x \neq 0$에서의 값을 추정할 수 있다.

 

Q. $n$이 무한대가 되면 멱급수 $p_{\infty}(x)$가 원래 함수 $f(x)$와 같아진다는 보장이 있을까?

 

---

 

아래는 근사다항식의 몇 가지 성질이다.

 

$f(x) \sim p_n(x)$이면 $f'(x) \sim p'_n(x)$이고, $F(x) \sim P_n(x)$이다. 여기서 $F(x)$와 $P_n(x)$는 각각 $f(x)$와 $p_n(x)$의 원시함수이다.

 

$f(x) \sim p_n(x)$이면 $f(ax^m)$의 $mn$차 근사다항식은 $p_n(ax^m)$이다.

 

$f(x) \sim p_n(x)$, $g(x) \sim q_n(x)$이면 $f(x)g(x)$의 $n$차 근사다항식은 $p_n(x)q_n(x)$의 $n$차 이하의 항만 취한 것이다. 여기서 주목할 점은 $f(x)g(x)$의 $n^2$차 근사다항식이 $p_n(x)q_n(x)$가 아니라는 점이다. 예를 들어,

 

$$e^x \sim 1 + x + \frac{1}{2}x^2$$

 

이지만,

 

$$\left(1 + x + \frac{1}{2}x^2 \right)^2 = 1 + 2x + 2x^2 + x^3 + \frac{1}{4}x^4$$

 

인 반면,

 

$$e^{2x} \sim 1 + 2x + 2x^2 + \frac{4}{3}x^3 + \frac{2}{3}x^4$$

 

으로, 둘은 2차까지만 일치함을 볼 수 있다.

 

---

 

예) $f(x) = \ln (1+x)$의 도함수는 아래와 같다.

 

\begin{align}
f'(x) &= (1+x)^{-1} \\
f''(x) &= -(1+x)^{-2} \\
f'''(x) &= 2(1+x)^{-3} \\
\vdots \\
f^{(n)}(x) &= (-1)^{n-1}(n-1)!(1+x)^{-n} \\
\end{align}

 

따라서 $\ln(1+x)$의 $n$차 근사다항식은 아래와 같다.

 

$$
\ln(1+x) \sim x - \frac{1}{2} x^2 + \frac{1}{3} x^3 - \dots + \frac{(-1)^{n-1}}{n} x^n
$$

 

근사다항식의 성질에 의해 양변을 미분할 수 있다.

 

$$\frac{1}{1+x} \sim 1 - x + x^2 - x^3 + ... + (-1)^{n-1} x^{n-1}$$

 

우변의 근사다항식은 무한차수까지 계속할 수 있지만, $|x|<1$일 때에만 수렴한다. 이 사실은 뒤에서 한번 더 살펴볼 것이다.

 

Q. 방금 보았듯이, 무한차수 근사다항식은 항상 수렴한다는 보장이 없다. 그렇다면 언제 $f(x)$와 $p_\infty(x)$가 같아질까?

 

---

 

미분가능한 함수 $f(x)$가 주어져있을 때, 아래의 두 함수에

 

$$y = f(x) - f(0) \qquad y=x$$

 

구간 $[0, x]$에서 코시의 평균값 정리를 적용하면 어떤 $c\in(0, x)$에 대해 아래를 만족한다.

 

$$\frac{f(x)-f(0)}{x-0} = \frac{f'(c)}{1}$$

 

이것은 사실 $f(x)$의 1차 근사식을 도출한 것과 같다.

 

$$f(x) = f'(c)x + f(0)$$

 

이번에는 $f(x)$에서 1차 근사식을 뺀 것과 $y = x^2$에

 

$$y = f(x) - f(0) - f'(0)x \qquad y = x^2$$

 

똑같이 $[0, x]$ 구간에서 코시의 평균값 정리를 적용해보면, 어떤 $c_1\in(0, x)$에 대해 아래를 만족한다.

 

$$\frac{f(x)-f(0)-f'(0)x}{x^2-0} = \frac{f'(c_1)-f'(0)}{2c_1}$$

 

여기서 아래의 두 함수에 대해

 

$$y = \frac{f'(x)-f'(0)}{2} \qquad y = x$$

 

이번에는 $[0, c_1]$ 구간에서 코시의 평균값 정리를 적용해보면,

 

$$\frac{f'(c_1)-f'(0)}{2(c_1-0)} = \frac{f''(c_2)}{2}$$

 

를 만족하는 어떤 $c_2\in(0, c_1)$이 존재한다. 정리해보면, 어떤 $c_2\in(0, x)$에 대해 아래 식이 성립한다.

 

$$\frac{f(x)-f(0)-f'(0)x}{x^2} = \frac{f''(c_2)}{2}$$

 

즉, $f(x)$에서 $f(x)$의 1차 근사다항식을 빼면 어떤 $c_2 \in (0, x)$에 대해서 아래 식이 성립한다.

 

$$f(x)-f(0)-f'(0)x = \frac{f''(c_2)}{2}x^2$$

 

이 식은 근사다항식이 아니라 정확한 등식임에 주목하라.

 

이 과정을 일반화하면 아래와 같다. $x=0$을 포함하는 열린 구간 $S$에서 $(n+1)$번 미분가능한 함수 $f(x)$와 임의의 $x\in S$에 대해

 

$$f(x) - f(0) - f'(0)x - \frac{f''(0)}{2!}x^2 - ... - \frac{f^{(n)}(0)}{n!}x^n = \frac{f^{(n+1)}(c)}{(n+1)!}x^{n+1}$$

 

를 만족하는 $c\in(0, x)$가 존재한다. 이 식을 $f(x)$에 대해서 쓰면 아래와 같은데,

 

$$f(x) = f(0) + f'(0)x + \frac{f''(0)}{2!}x^2 + ... + \frac{f^{(n)}(0)}{n!}x^n + \frac{f^{(n+1)}(c)}{(n+1)!}x^{n+1}$$

 

이것을 Taylor polynomial이라고 부른다. 우변의 마지막 항을 제외하면 $n$차 근사다항식과 같음을 알 수 있다. 우변 마지막 항을 $n$차 잉여항이라고 부르며, $R_n(x)$로 표기한다.

 

---

 

앞서 언급했던 질문을 다시 보자. $f(x)$의 $n$차 근사다항식은 $n$을 무한대로 보내면 멱급수 $p_\infty(x)$가 된다. 정의역의 어떤 $x$에서 $f(x) = p_\infty(x)$가 되려면, $n\to\infty$일 때 Taylor polynomial의 잉여항이 0이 되어야 한다.

 

구간 $[0, x]$에서 $|f^{(n+1)}(t)|$의 최대값을 $M_n(x)$라 하자. 다음 식이 성립한다.

 

$$\left| R_n(x) \right| \le M_n(x) \frac{|x|^{(n+1)}}{(n+1)!}$$

 

예를 들어 $f(x) = \sin(x)$로 두면 $M_n(x) \le 1$이므로

 

$$\left| R_n(x) \right| \le \frac{|x|^{(n+1)}}{(n+1)!}$$

 

이고, 모든 실수 $x$에 대해서

 

$$\lim_{n\to\infty} |R_n(x)| = 0 $$

 

이다. 따라서

 

$$ \sin x = \sum_{n=0}^{\infty} \frac{(-1)^n}{(2n+1)!}x^{(2n+1)}$$

 

라고 쓸 수 있다. 아래는 $\sin x$의 Taylor polynomial이 $\sin x$로 수렴하는 모습이다.

 

 

figure, ax = axes;
hold on, box off
ax.XAxisLocation = 'origin';
ax.YAxisLocation = 'origin';

x = linspace(-10, 10);

fplot(@sin, minmax(x), 'r', LineWidth=2)
p = plot(x, x, 'b', LineWidth=2);
ylim([-2, 2])
l = legend('sin(x)', '0-th order Taylor');

pause(1)

for n = 1:15
    p.YData = p.YData + (-1)^n/factorial(2*n+1) * x.^(2*n+1);
    l.String{2} = sprintf('%d-th order Taylor', n);
    pause(0.3)
end

 

---

 

앞에서 봤던 $f(x) = \ln(1+x)$를 다시 보자. 일단 정의역은 $x>-1$이다. 아래 식은 $t \neq -1$에서 항상 성립한다.

 

$$
\frac{1}{1+t} = 1 - t + t^2 - ... + (-1)^{n-1}t^{n-1} + \frac{(-1)^nt^n}{1+t}
$$

 

위 식을 0부터 $x$까지 적분하면 아래와 같다. (단, $x>-1$)

 

$$
\ln(1+x) = x - \frac{1}{2}x^2 + \frac{1}{3}x^3 - ... + \frac{(-1)^{n-1}}{n}x^n + (-1)^n \int_0^x \frac{t^n}{1+t} dt
$$

 

우변의 마지막 항을 제외하면 $\ln(1+x)$의 $n$차 근사다항식과 같으므로, 마지막 항은 잉여항 $R_n(x)$이다. 어느 $x$ 범위에서 $n\to\infty$일 때 잉여항이 $0$이 될까?

 

$x>1$이면, $a>2x$를 만족하는 어떤 $a$에 대해

 

$$
\left| R_n(x) \right| = \int_0^x \frac{t^n}{1+t} dt \ge \int_0^x \frac{t^n}{a}dt = \frac{1}{a} \frac{x^{n+1}}{n+1}
$$

 

이므로

 

$$
\lim_{n\to\infty} \left| R_n(x) \right| = \infty
$$

 

이다. 즉, $x>1$에서는 잉여항이 수렴하지 않으므로 $\ln(1+x)$의 무한차수 근사다항식의 값은 $\ln(1+x)$와 같지 않다.

 

$x\in[0, 1]$이라면,

 

$$
\left| R_n(x) \right| = \int_0^x \frac{t^n}{1+t} dt \le \int_0^x \frac{t^n}{1}dt = \frac{x^{n+1}}{n+1}
$$

 

이므로,

 

$$
\lim_{n\to\infty} \left| R_n(x) \right| = 0
$$

 

이다. 따라서 이 범위의 $x$에 대해서는 잉여항이 $0$으로 수렴하므로 $\ln(1+x)$의 무한차수 근사다항식의 값은 $\ln(1+x)$와 같다.

 

$x\in(-1, 0)$이면, 어떤 $a \in (-1, x)$에 대해

 

$$
\left| R_n(x) \right| = \int_0^x \frac{|t|^n}{1+t} dt \le \int_0^x \frac{|t|^n}{1+a}dt = \frac{1}{1+a}\frac{|x|^{n+1}}{n+1}
$$

 

이므로,

 

$$
\lim_{n\to\infty} \left| R_n(x) \right| = 0
$$

 

이다. 따라서 이 범위의 $x$에 대해서는 잉여항이 0으로 수렴하므로 $\ln(1+x)$의 무한차수 근사다항식의 값은 $\ln(1+x)$와 같다.

 

종합하자면, $\ln(1+x)$의 $n$차 잉여항은 $x\in(-1, 1]$일 때에는 0으로 수렴하고 그 외에는 발산한다. 즉, $\ln(1+x)$는 $(-1, 1]$ 범위에서 $p_\infty(x)$와 같다. 아래는 이 함수의 수렴 영역을 보여주고 있다.

 

 

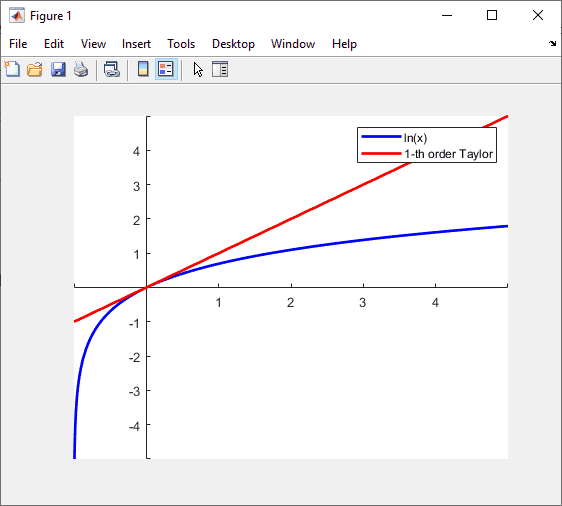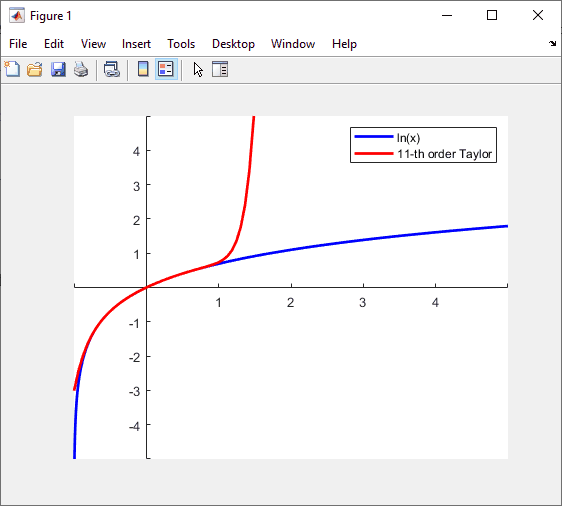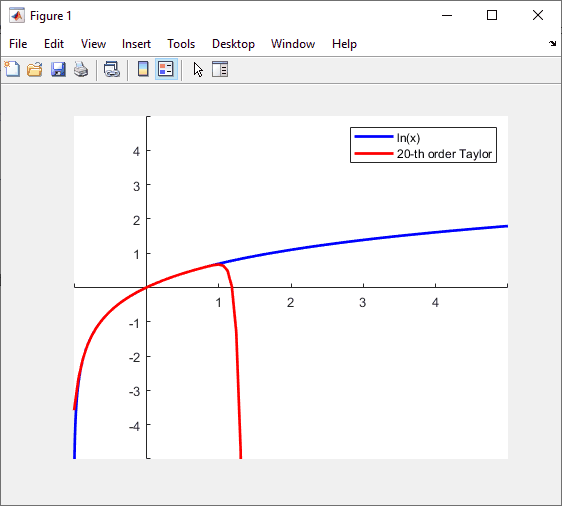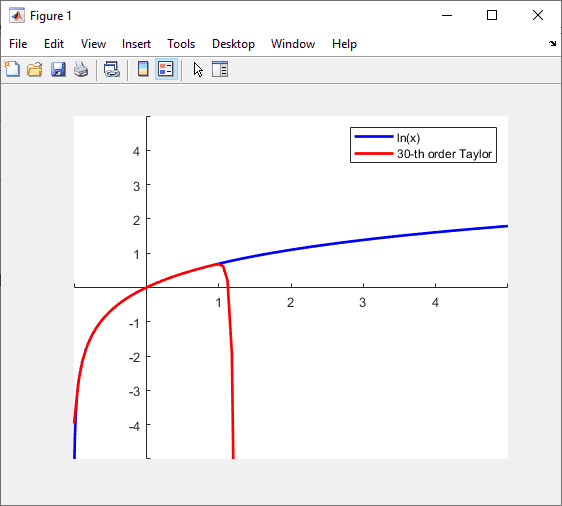
figure, ax = axes; 
hold on, box off
ax.XAxisLocation = 'origin';
ax.YAxisLocation = 'origin';

x = linspace(-0.999, 5);

fplot(@(x) log(1+x), 'b', LineWidth=2)
pn = @(n) (-1)^(n-1)/n*x.^n;
p = plot(x, pn(1), 'r-', LineWidth=2);
ylim([-5, 5])
l = legend('ln(x)', '1-th order Taylor');

pause(1)

for n = 2:30
    p.YData = p.YData + pn(n);
    l.String{2} = sprintf('%d-th order Taylor', n);
    pause(0.3)
end

 

---

 

함수 $f(x)$가 무한번 미분가능하다면,

 

$$
T(x) := \sum_{n=0}^{\infty} \frac{f^{(n)}(0)}{n!}x^n = f(0) + f'(0)x + \frac{f''(0)}{2!}x^2 + ... + \frac{f^{(n)}(0)}{n!}x^n + ...
$$

 

를 $f(x)$의 $x=0$에서의 테일러 급수(Talyor series)라고 부른다. 이것을 $x = p$로 일반화하면 다음과 같다.

 

$$
T(x) := \sum_{n=0}^{\infty} \frac{f^{(n)}(p)}{n!}(x-p)^n = f(p) + f'(p)(x-p) + \frac{f''(p)}{2!}(x-p)^2 + ... + \frac{f^{(n)}(p)}{n!}(x-p)^n + ...
$$

 

$f(x)$가 $T(x)$와 같을 필요충분조건은

 

$$\lim_{n\to\infty}R_n(x) = 0 $$

 

이다. $f(x)$가 무한번 미분 가능하다면 $f(x)$의 테일러 급수 $T(x)$는 항상 얻을 수 있다. 하지만 $T(x)$가 계산된다고 하여 $f(x) = T(x)$를 보장하지는 않는다. 이미 앞에서 $\ln(1+x)$의 경우를 보았다. 이 함수는 $x\in(1, \infty)$에서 $f(x)$와 $T(x)$가 같지 않았다.

 

---

 

이번엔 $x>0$인 모든 점에서 $f(x) \neq T(x)$인 경우를 보겠다. 아래와 같이 정의된 함수 $f(x)$가 있다.

 

$$f(x)=\begin{cases}
e^{-1/x} & (x > 0) \\
0 & (x \le 0)
\end{cases}$$

 

https://en.wikipedia.org/wiki/Non-analytic_smooth_function

 

 

이 함수의 도함수는 아래와 같은데,

 

$$f^{(n)}(x)=\begin{cases}
\cfrac{P_n(x)}{x^{2n}}f(x) & (x > 0) \\
0 & (x \le 0)
\end{cases}$$

 

여기서 $P_n(x)$는 아래와 같이 재귀적으로 정의되는 함수이다.

 

$$P_{n+1}(x) = x^2 P'_n(x) - (2nx-1) P_n(x)$$

 

이 함수의 $x=0$에서의 $n$차 도함수는 모두 0이다. 증명은 위키피디아 페이지로 갈음한다. 따라서 이 함수는 $(-\infty, 0]$에서만 $T(x) = f(x)$이다.

 

이 함수는 대표적인 비해석적 함수(non-analytic function)이다. 해석적 함수(analytic function)란 정의역의 모든 점의 근방에서 테일러 급수가 원래의 함수값으로 수렴하는 함수를 말한다. 위에서 본 함수는 $x>0$인 모든 점에서 이 조건을 만족하지 않는다. 심지어 모든 점에서 무한번 미분 가능함(smooth)에도 불구하고 비해석적이라는 특징을 갖는다.

 

---

 

이번 글에서는 테일러 급수의 수렴 조건에 대해서 알아보았다.

 

끗