티스토리 뷰

지수함수의 도함수
일단 임의의 양의 실수

이제
여기서
식 (1)을 보면 지수함수는 특별한 함수임을 알 수 있다. 도함수가 자기 자신의 상수배가 된다. 그렇다면
지수함수(exponential)를 대표한다는 의미로
그렇다면
지수함수의 역함수
한편
우리말로 풀어 쓰자면

두 그래프는 역함수 관계이므로
로부터
임을 알 수 있다.
이 되어,
log
가 성립한다. 증명은 아래와 같다.
e
이제
이고, 식 (6)으로부터
이다.
가 성립하며,
이다.
e
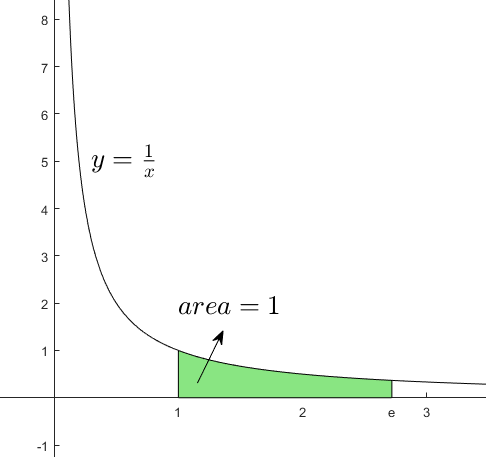
양변을 1에서
이 되며, 특별히
가 된다. 즉,
게으른
'mathe' 카테고리의 다른 글
| 수학의 즐거움 멤버십 인터뷰 전문 (2) | 2023.03.19 |
|---|---|
| 나는 수학을 왜 공부하는가 (0) | 2023.03.19 |
| 유리수 가정으로 시작하지 않는 √2의 무리수 증명 (0) | 2023.02.10 |
| XOR란? (0) | 2023.01.27 |
| 어린 왕자와 삼각형의 내각의 합 (0) | 2023.01.18 |
