공허참이란?

 

 

 

초간단요약

 

두 명제 A와 B에 대해서, 합성명제인 "A이면 B이다"는 다음과 동치이다.

"A를 만족하는 진리집합은 B를 만족하는 진리집합의 부분집합이다."

 

예: $0<x<1$이면 $0<x<2$가 참인 이유:

$A=\{x|0<x<1\}$과 $B=\{x|0<x<2\}$에 대해서 $A\subset B$가 참임

 

그럼 "A이면 B이다"에서 A가 거짓이면 어떻게 될까?

예: $1<x<0$이면 $0<x<2$는 참일까 거짓일까?

 

위 방법을 이용한다면, $A=\{x|1<x<0\}$는 공집합이다. 공집합은 모든 집합의 부분집합이다. 따라서 이 명제는 항상 참이다. 이렇게 전건이 거짓임으로 인해서 참이 되는 명제를 공허참vacuous truth라고 부른다.

 

어떤 가치가 있는 논증인지는 잘 모르겠다. 논리적 일관성을 위한 것인가 싶기도 하다.

 

---

 

추가로 고민해본 것들을 몇 가지 적어본다. (24년 6월 16일)

 

• 지금까지 잘못 생각한 것: $p\to q$에서 $p$가 거짓이면 $q$가 참이 된다고 생각해왔다.

• 그거 아니다. $p$가 거짓일 때 참이 되는 것은 $p\to q$이다.

• 다만, $p$가 항상 거짓일 때에는 납득이 되는데(예: $|x|<0$) 그렇지 않을 때에는 여전히 모르겠다.

 

• $p\to q$에서 나올 수 있는 경우의 수는 모두 4가지이다.

• $p$와 $q$가 모두 참일 때에는 $p\to q$도 참이어야 할 것 같다.

• 예를 들어 $p:x=1$, $q:x+1=2$이면 $p\to q$는 참이다.

• 비슷하게 $p$가 참이고 $q$가 거짓이면 $p\to q$는 거짓이어야 할 것 같다.

• 예를 들어 $p:x=1$, $q:x+1=3$이면 $p\to q$는 거짓이다.

 

 

• 문제는 $p$가 거짓일 때이다.

• 이것은 대우명제로 해결해보자.

• $p\to q$와 $\sim q\to \sim p$의 진리값은 같다.

• 순환논리일지도 모르겠으나 일단 패스, 지금은 일관성만 보자.

• 이것을 이용하면 아래와 같이 표를 확장할 수 있다.

 

 

 

• ①과 ②는 $p\to q$를 그대로 가져온 것이다.

• ③은 $T\to T$이므로 $T$이다.

• ④는 ③을 그대로 가져온 것이다.

• 남은 두 칸은 대우명제만으로는 해결할 수 없다.

• 다른 방법으로 해결해보자.

 

• $p\to q$가 명백한 거짓일 때는 어떤 경우일까?

• 예를 들어 $p:x=1$, $q:x+1=3$이면 왜 $p\to q$가 거짓이라고 말하는가?

• 그 이유는 $p$가 참일 때 $q$가 거짓이기 때문이다.

• 다시 말해 $p\to q$가 거짓이면 $p\wedge \sim q$는 참이다.

• 이것을 아래와 같이 쓰자.

 

$$\sim (p\to q)\equiv (p\wedge \sim q)$$

 

• 실제로 귀류법은 $p\wedge \sim q$이 거짓임을 보여 $p\to q$를 보이는 방법이다.

• 그렇다면 $p\to q$는 아래와 같이 쓸 수 있게 된다.

 

$$(p\to q)\equiv (\sim p\vee q)$$

 

• 즉 $p$가 거짓이면 $p\to q$는 무조건 참이고, $p$가 참이면 $q$와 $p\to q$는 같다.

• 이것을 이용하여 표를 마저 채우면 아래와 같다.

 

 

 

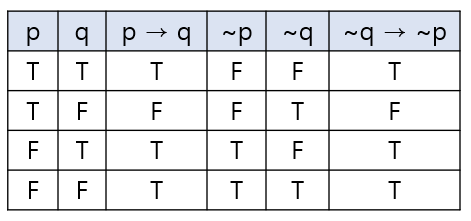
• 납득은 되지 않더라고 적어도 논리적 일관성은 확보할 수 있게 된다.

• $p\to q$의 대우명제도 같은 방식으로 따져보면,

 

$$(\sim q\to \sim p)\equiv (q\vee \sim p)\equiv (\sim p\vee q)\equiv (p\to q)$$

 

• 역시 일관적임을 알 수 있다.

 

• 여전히 불편하다면, 또 다른 방향으로 생각해보자.

• $p$가 항상 거짓인 $p\to q$를 아무거나 하나 만들어보자.

 

$$|x|<0\to x=0$$

 

• Nonsense로 보이지만, 일단 그런건 따지지 말아보자.

• 이 명제는 아래의 대우명제와 진리값이 같아야 한다.

 

$$x\ne 0\to |x|\ge 0$$

 

• 이 대우명제는 참이다.

• 그리고 참일 수밖에 없다. $p$가 항상 거짓이고 $\sim p$는 항상 참이기 때문이다.

• 따라서 $p$가 항상 거짓이라면 $p\to q$는 참으로 두는 것이 타당해보인다.

• 어디까지나 일관성을 갖기 위한, 즉 예외를 허용하기 않기 위한 방법으로 보인다.

 

---

 

또 추가로 고민해본 것을 적어둔다. (24년 6월 27일)

 

• 귀류법은 아래와 같이 진행된다.

 

1. $P\to Q$를 보이는 대신, $\sim Q$를 가정한다.

2. $P$는 이미 가정했으므로, $P\wedge \sim Q$를 확인해본다.

3. 결과가 모순이면(False이면) $P\to Q$는 참이다.

 

헷갈리는 포인트들이 있다.

 

• $P$가 참이면서 동시에 $Q$가 거짓일 수 없으면 왜 $P\to Q$가 참이 되는가?

• 논리적 정합성 말고, 자연스럽고 당연히 받아들여지는 연역적 과정인지가 불확실하다.

• $P\to Q$와 $\sim (P\wedge \sim Q)$이 동치라는 것이 갑자기 불편하고 인위적으로 느껴진다.

• $P\to Q$에서 이미 $P$를 가정했다고 했는데 ($P$ is True)

• $P\wedge \sim Q$를 판단할 때에도 $P$가 참이라고 가정한 것인가?

• $P$가 어떻게 조건명제의 전건과 합성명제의 요소 사이를 마음대로 왔다갔다 할 수 있나?

 

• 나무위키를 보면

• $P\to Q$와 $P\wedge Q$는 동치가 아니라고 한다.

• $P\wedge Q$가 참이면 $P\to Q$도 참인 것은 맞지만

• $P\to Q$가 참이어도 $P\wedge Q$는 거짓일 수 있다.

• 그런데 그런 경우는 전제조건 $P$가 이미 거짓일 때뿐이지 않은가?

• 귀류법으로 $P\to Q$를 보일 때에는 이미 $P$를 참이라고 가정하지 않는가?

• 그렇다면 귀류법으로 $P\to Q$를 보이는 것은 $P\wedge Q$를 보이는 것과 같은가?

• 그렇다면 $P\wedge \sim Q$를 보이는 것은 $P\to \sim Q$를 보이는 것과 같은가?

• 예를 들어

• $P:x$가 4의 배수이다.

• $Q:x$가 짝수이다.

• 이 경우 $P\wedge \sim Q$는 "$x$는 4의 배수이고 홀수이다."이므로 거짓이고

• $P\to \sim Q$는 "$x$가 4의 배수이면 홀수이다."이므로 역시 거짓이다.

• 하지만 그렇다고 $P\wedge \sim Q$와 $P\to \sim Q$가 같다고 볼 수 있나? 특별한 케이스일지도?

• 아니면 명제 자체가 성립하지 않는 것인가?

 

• 귀류법에서 $(P\wedge \sim Q)\equiv F$를 보이는데

• 이것은 $(P\to \sim Q)\equiv F$를 보이는 것과 왜 자꾸 같다고 느껴지는가? (논리표로는 다름)

• $P$를 어차피 참으로 가정했다면, $Q$만 보면 되는 건가?

 

쓰다보니 더 혼란스러워진다.

너무 깊이 파지는 말아야겠다.

 

---

 

약간 재밌는 표현을 찾아서 적어둔다. (24년 6월 28일)

 

아래는 항진명제이다.

 

$$x<2\Rightarrow x<4$$

 

항진명제란 항상 참인 명제를 말한다. 따라서 위 명제는 (논의 영역에 있는) 어떤 $x$에 대해서도 참이다.

• $x=1$이면 $T\Rightarrow T$가 된다.

• $x=3$이면 $F\Rightarrow T$가 된다.

• $x=5$이면 $F\Rightarrow F$가 된다.

• 항진명제이므로 위 세 가지는 모두 참이다.

• 즉, $P\to Q$가 거짓일 때에는 $P$가 참이고 $Q$가 거짓일 때 뿐이다.

 

뭔가 속는 것 같다...

 

 

끗