1/√(1-x^2)의 적분 = pi/2

 

 

아래 부정적분은,

 

$$\int_{0}^{1} \frac{dx}{\sqrt{1-x^2}}$$

 

$x=\sin {u}$로 치환하여 풀 수 있다.

 

$$\int_{0}^{1} \frac{dx}{\sqrt{1-x^2}} = \int_{0}^{\pi/2} \frac{\cos u \: du}{\cos u} = \frac{\pi}{2}$$

 

왜 뜬금없이 원주율이 나올까?

 

 

 

$P(P_x, P_y)$: $y=\sqrt{1-x^2}$ 위의 한 점

$A(0, P_y)$, $P$에서 $y$축에 내린 수선의 발

$B(P_x, 0)$, $P$에서 $x$축에 내린 수선의 발

$C(P_x, 1/\sqrt{1-P_x^2})$: $\overline{BP}$의 연장선이 $y=1/\sqrt{1-x^2}$와 만나는 점

 

각 선분의 길이는 아래와 같다.

 

\begin{align}
\overline{PA} &= P_x \\
\overline{PB} &= P_y \\
\overline{PC} &= \frac{1}{P_y} - P_y = \frac{1-P_y^2}{P_y} = \frac{P_x^2}{P_y}
\end{align}

 

이제 다음과 같은 미소선분과 면적을 생각하자.

 

 

 

$x=0$에서 $x=1$까지 $dA_x$를 적분하면 사분원의 면적이므로 $\pi/4$가 된다. $dA_y$도 마찬가지이다.

 

$$\int_{x=0}^{x=1} dA_x = \int_{y=0}^{y=1} dA_y = \frac{\pi}{4}$$

 

$dA_x$와 $dA_y$의 면적 비율은 다음과 같다.

 

$$\frac{dA_y}{dA_x} = \frac{P_x \: dy}{P_y \: dx}$$

 

$dA_y$와 $dA_f$의 면적 비율은 다음과 같다.

 

$$\frac{dA_f}{dA_y} = \frac{(P_x^2/P_y)dx}{P_x \: dy} = \frac{P_x \: dx}{P_y \: dy}$$

 

그런데

 

$$\frac{P_y}{P_x} = \frac{dx}{dy}$$

 

이므로 결과적으로 $dA_f = dA_y$이다. 따라서 $y=0$에서 $y=1$까지 $dA_y$를 적분한 것과 $x=0$에서 $x=1$까지 $dA_f$를 적분한 것은 그 값이 같을 것이다. 정리하면,

 

$$\int_{x=0}^{x=1} dA_x = \int_{y=0}^{y=1} dA_y = \int_{x=0}^{x=1} dA_f = \frac{\pi}{4}$$

 

이다. 이것을 그림으로 표현하면 아래와 같다.

 

 

 

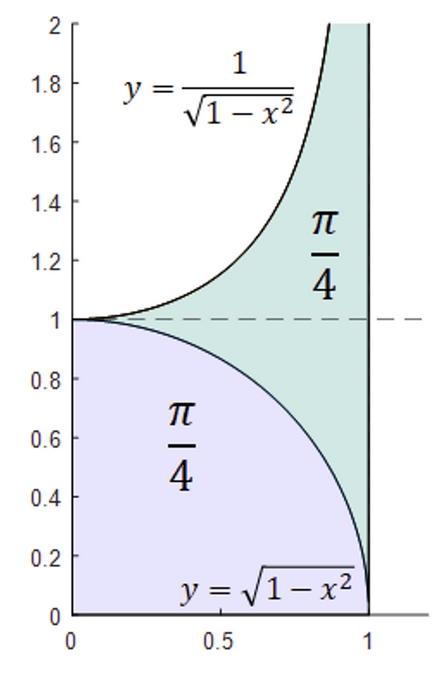
두 색칠된 영역의 면적은 $\pi/4$로 같으며, 원래 문제였던

 

$$\int_{0}^{1} \frac{dx}{\sqrt{1-x^2}}$$

 

는 두 영역의 합과 같으므로 값은 $\pi/2$가 된다.

 

위 그림을 그린 매트랩 코드

 

x = linspace(0, 1-1e-3);
y1 = sqrt(1-x.^2);
y2 = 1./sqrt(1-x.^2);

figure, hold on,
plot(x, y1)
plot(x, y2)
xline(1, 'k--')
yline(1, 'k--')

patch([x, flip(x)], [zeros(size(x)), flip(y2)], 'b', FaceAlpha=0.1)
patch([x, flip(x)], [y1, flip(y2)], 'g', FaceAlpha=0.1)

axis equal
xlim([0, 1.2])
ylim([0, 2])

 

끗