자연수를 순서대로 무한분수로 배열해서 √2 만들기

 

 

abakcus.com

 

 

이게 뭔가 싶었는데, 계산해보니까 정말 된다.

 

import numpy as np

val = 1/2
i = 2

for _ in range(20):
    seq = np.arange(2**(i-1)+1, 2**i+1)
    while len(seq) > 1:
        seq = seq[0::2] / seq[1::2]
    val = val / seq[0]
    print(val**2)
    i += 1

 

0.4444444444444444
0.48999999999999994
0.4986800792562108
0.49988285033446983
0.49999341444424916
0.4999997749586686
0.49999999545844154
0.4999999999470098
0.4999999999996485
0.49999999999999895
0.4999999999999985
0.4999999999999952
0.49999999999999456
0.4999999999999845
0.49999999999998296
0.49999999999998046
0.5000000000000012
0.5000000000000162
0.5000000000000376
0.5000000000000882

 

 

위키피디아에는 $\sqrt{2}$를 만드는 여러 무한곱이 있지만, 이것과 똑같은 것은 없다.

 

 

https://en.wikipedia.org/wiki/Square_root_of_2

 

 

혹시나 이 자연수 무한분수를 잘 재배치하면 이 식들 중 하나로 만들 수 있지 않을까 시도해봤으나 실패. 특히 두 번째 식은 정말 비슷하지만 값이 다른 항들이 나온다.

 

안될 때는 검색이다. 이미지로 검색하니까 딱 하나가 나온다. 그것도 트위터가(...).

 

https://x.com/abakcus/status/1602485217360486400

 

 

아래는 이 트윗의 댓글 중 하나를 참고한 것이다. 대부분 댓글의 내용을 그대로 따라갔으나 약간 추가된 것이 있다.

 

---

 

자연수 분수 수열의 첫 4개 항은 아래와 같다.

 

 

 

이 수열의 극한을 아래와 같이 써보자.

 

 

여기서 $S_n=\{1,-1\}$이다. 수열 $\{S_n\}$의 규칙을 찾아야 한다. 4번째 항의 각 분수가 어떤 식으로 올라(?)가는지 관찰해보면,

 

 

각 분수 $(2n+1)/(2n+2)$는 $1/2$ 옆으로 올라가기 위해 몇 번의 뒤집힘을 겪는데, 뒤집히는 횟수는 $(2n+1)/(2n+2)$이 최상단으로 가기 위해 넘어가는 선(나누기 기호)을 세되 앞에서 넘은 것보다 긴 것만 세면 된다. 예를 들어 $7/8$은 아래와 같이

 

 

 

$5/6$ 옆으로 가면서 한 번, $(1/2)/(3/4)$ 옆으로 가면서 또 한번, 총 2번의 뒤집힘을 겪는다. $1/2$와 $3/4$ 사이의 선은 이미 계산되어 있으므로 $7/8$을 뒤집지 않는다. 2번 뒤집히므로 최종 식에서 $(7/8{)}^1$이 곱해진다. $9/10$은

 

 

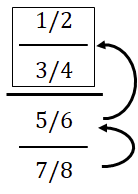
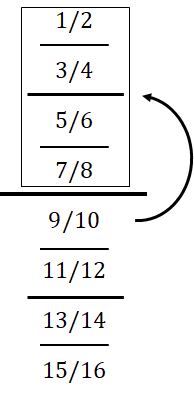
한 번만 뒤집히면 된다. 가장 긴 나누기 기호 위는 이미 한 덩어리로 계산되어 있기 때문이다. 즉, 이미 넘어간 선보다 더 짧은 것은 세지 않는다. 넘어간 선보다 짧은 것은 이미 계산되어 있기 때문이다. 그래서 $9/10$은 한 번만 뒤집히고 최종 식에서 $(9/10{)}^{-1}$이 곱해진다. 이제 $S_n$은 아래와 같이 정의할 수 있다.

• $(2n+1)/(2n+2)$가 최상단으로 가기 위해 짝수번 뒤집히면 $S_n=+1$

• $(2n+1)/(2n+2)$가 최상단으로 가기 위해 홀수번 뒤집히면 $S_n=-1$

 

Thue-Morse sequence $\{t_n\}$이라는 것이 있다. 아래와 같이 정의된다.

• $n$을 2진수로 표현냈을 때 1이 짝수번 있으면 0

• $n$을 2진수로 표현냈을 때 1이 홀수번 있으면 1

https://en.wikipedia.org/wiki/Thue%E2%80%93Morse_sequence

 

 

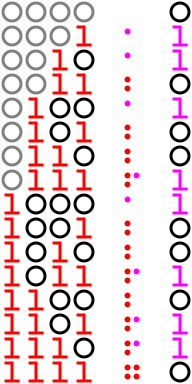
Lemma. $S_n=(-1{)}^{t_n}$

 

이 lemma가 말하는 것은, $(2n+1)/(2n+2)$가 최상단으로 가기 위해 뒤집히는 횟수와 $n$의 2진수 표현에 나타난 1의 횟수가 mod 2로 같다는 것이다. 사실 mod 2로만 같은 것이 아니라 그냥 두 수는 같다. 증명은 수학적 귀납법으로 가능하다. 증명의 스케치만 적어둔다. $1/2$부터 $7/8$까지 필요한 값들을 모두 적어보면 아래와 같다.

 

 

 

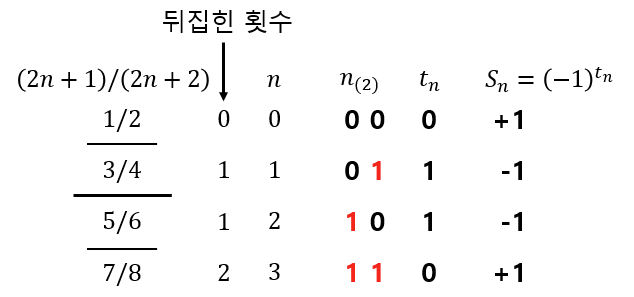
빨간 1이 어떻게 적혀있는지를 보면, 넘어야 할 선의 길이 순서 해당되는 위치가 1임을 알 수 있다. 예를 들어

• $3/4$는 가장 짧은 선을 한번만 넘으면 되므로 $(01)$

• $5/6$은 두 번째로 짧은 선을 한번만 넘으면 되므로 $(10)$

• $7/8$은 가장 짧은 선을 한번 넘고 두 번째로 짧은 것도 한번 넘어야 하므로 $(11)$

가 된다. 여기에 $9/10$부터 $15/16$까지 4개를 추가하면 아래와 같다.

 

 

 

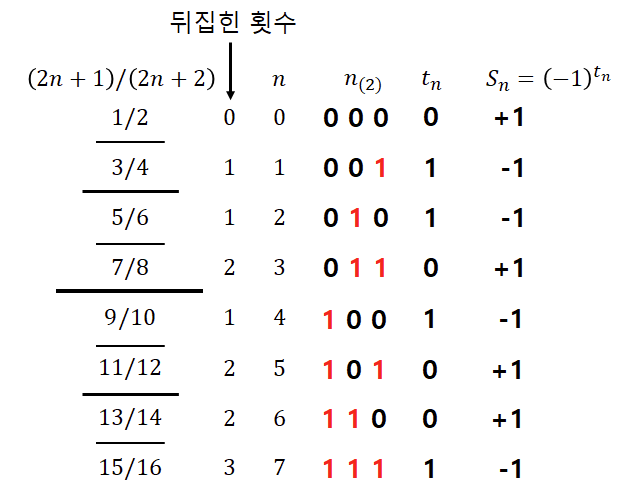
새로 추가된 항들의 $t_n$과 $S_n$은 앞의 4개와 정확히 반대가 된다. 왜냐하면

• 2진수 표현에서 맨 앞 1이 일괄적으로 추가되었기 때문

• 넘어야 할 선이 앞의 4개보다 정확히 1개 늘어나기 때문

이다. 같은 이유로 뒤집힌 횟수가 $n_{(2)}$에서 1의 개수와 정확히 같아진다.

 

결국 각 항(분수)이 최상단으로 가기 위해 넘어야 할 횟수는 $t_n$과 mod 2로 같고, 수학적 귀납법으로 $S_n=(-1{)}^{t_n}$임을 알 수 있다.

 

수열 $S_n$은 아래의 특징을 갖는다.

 

1. $S_{2n}=S_n$
2. $S_{2n+1}=-S_{2n}$

 

1. $S_{2n}=(-1{)}^{t_{2n}}$인데, $2n$의 2진수 표현과 $n$의 2진수 표현은 1의 개수가 같다.

2. $2n$의 가장 오른쪽 자릿수는 0이므로, $2n+1$과 $2n$은 1의 개수가 다르다.

 

 

이제 원래 계산하고자 했던 수열의 극한을 다시 보자.

 

 

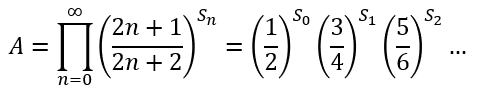
아래와 같은 새로운 수열을 만들어보자.

 

 

 

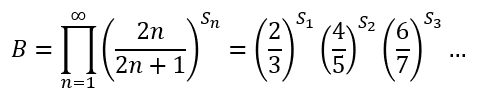
두 수열의 곱은 아래와 같고

 

 

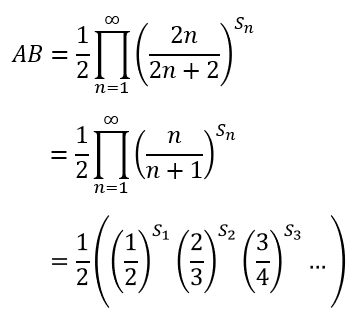
여기서 짝수번 째, 홀수번 째 항들을 분리해보면 아래와 같이 쓸 수 있고

 

 

$S_n$의 성질을 이용하면

 

 

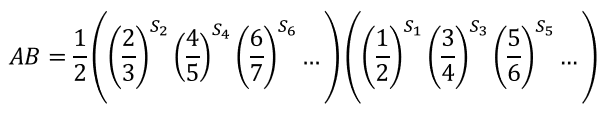
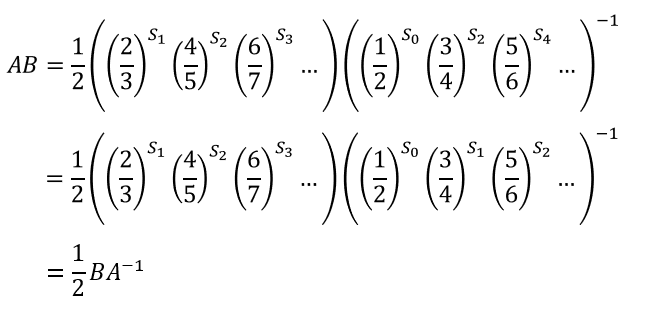
가 되어, 최종적으로 $A=\sqrt{2}/2$가 된다.

 

여기서 $A$와 $B$가 실수에서 수렴한다는 것을 보여야 하는데, 아까 그 트윗의 댓글을 참고하자. 아래 유튜브는 다른 방법으로 증명하는 것인데, 솔직히 이해를 못했다.