수학 귀신에 나온 내용들

https://ko.wikipedia.org/wiki/수학_귀신

 

 

사놓고 귀찮아서(...) 안 읽고 있던 수학귀신 책을 읽었다. 그냥 뭐 어린이 책이겠거니~하고 읽었으나 의외로 재밌는 내용들이 있었다. 몇 가지 기록으로 남겨두고 싶은 것들을 적어둔다.

 

---

 

1. 임의의 자연수는 최대 3개의 삼각수의 합이다. (증명)

 

몇 가지 예시들:

\begin{align}
51 &= 15 + 36\\
83 &= 10 + 28 + 45\\
12 &= 1 + 1 + 10\\
\end{align}

 

우선 $8n+3$ 꼴의 자연수는 항상 3개의 홀수 제곱수의 합으로 나타낼 수 있다.[1][2] 증명[3]은 너무 어려워서 이해를 포기했다(...). 이것을 받아들이면, $8n+3$은 아래와 같이 쓸 수 있다.

 

\begin{align}
8n+3 &= (2a+1)^2 + (2b+1)^2 + (2c+1)^2 \\
&= 4a(a+1) + 4b(b+1) + 4c(c+1) + 3
\end{align}

 

따라서 임의의 자연수 $n$은 아래와 같이 세 개의 삼각수의 합이다.

 

$$n = \frac{a(a+1)}{2} + \frac{b(b+1)}{2}  + \frac{c(c+1)}{2} $$

 

---

 

2. 연속된 두 삼각수의 합은 제곱수이다.

 

$$\frac{a(a+1)}{2} + \frac{(a+1)(a+2)}{2}=(a+1)^2$$

 

---

 

3. 파스칼의 삼각형의 $n$번째 줄의 합은 $2^n$이다.

 

단, 맨 윗 줄을 0번째로 정의한다.

 

https://www.mathsisfun.com/pascals-triangle.html

 

 

파스칼의 삼각형은 ${_n}C_r$들을 적은 것이다. $n$번째 줄은 $r$이 0부터 $n$까지 변할 때의 ${_n}C_r$ 값들이다. ${_n}C_r$은 $n$개 중 $r$개를 고르는 경우의 수이다. 따라서 ${_n}C_r$의 합은 $n$개 중 가능한 모든 조합의 수이므로, 각각을 고르거나 말거나 둘 중 하나이므로 모든 경우의 수는 $2^n$이다.

 

---

 

4. 파스칼의 삼각형에서 피보나치 수열을 찾을 수 있다.

 

https://www.mathsisfun.com/pascals-triangle.html

 

 

위 그림에서 같은 색으로 칠해진 숫자들을 더하면 피보나치 수열이 된다. 수학적 귀납법으로 증명할 수 있다. 즉,

 

\begin{align}{_n}C_n + {_{n+1}}C_{n-1} + {_{n+2}}C_{n-2} + \cdots {_{2n-1}}C_{1} + {_{2n}}C_{0} = F_{2n+1}
\\
{_{n+1}}C_n + {_{n+2}}C_{n-1} + {_{n+3}}C_{n-2} + \cdots {_{2n}}C_{1} + {_{2n+1}}C_{0} = F_{2n+2}
\end{align}

 

이면

 

\begin{align}
{_{n+1}}C_{n+1} + {_{n+2}}C_{n} + {_{n+3}}C_{n-1} + \cdots {_{2n+1}}C_{1} + {_{2n+2}}C_{0} = F_{2n+3}
\\
{_{n+2}}C_{n+1} + {_{n+3}}C_{n} + {_{n+4}}C_{n-1} + \cdots {_{2n+2}}C_{1} + {_{2n+3}}C_{0} = F_{2n+4}
\end{align}

 

임을 증명하면 된다. ${_{n}}C_{r-1} + {_{n}}C_{r} = {_{n+1}}C_{r}$을 이용하면 증명할 수 있다. 증명은 적기 귀찮아서 생략한다.

 

 

 

---

 

5. $n$명 중에서 3명을 고르는 경우의 수는 파스칼의 삼각형의 3번째 대각선을 보면 된다.

https://mathmonks.com/pascals-triangle

 

 

---

 

6. 피보나치 수열과 관련된 재밌는 사실들

 

자세한 내용은 다른 글에 적어두었다.

 

• 피보나치 수열의 첫 $n$개의 항을 더하고 1을 더하면 $n+2$번째 피보나치 수가 된다.

• $F_2$부터 $F_{2n}$까지 짝수번째 항을 모두 더하고 1을 더하면 $F_{2n+1}$이다.

• $F_3$부터 $F_{2n+1}$까지 홀수번째 항을 모두 더하고 1을 더하면 $F_{2n+2}$이다.

• 피보나치 수열의 연속된 두 항의 비율은 $(1+\sqrt{5})/2$이다. 첫 두 항을 아무렇게나 줘도 성립한다. (단, 둘 중 적어도 하나는 0이 아니어야 한다.)

 

---

 

7. 정사면체 토러스

 

이게 되네? (영상)

 

 

 

 

 

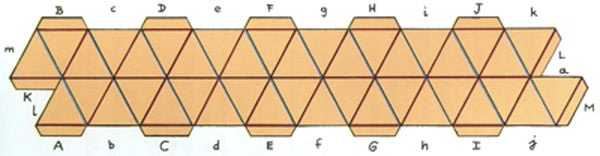
끗.