티스토리 뷰
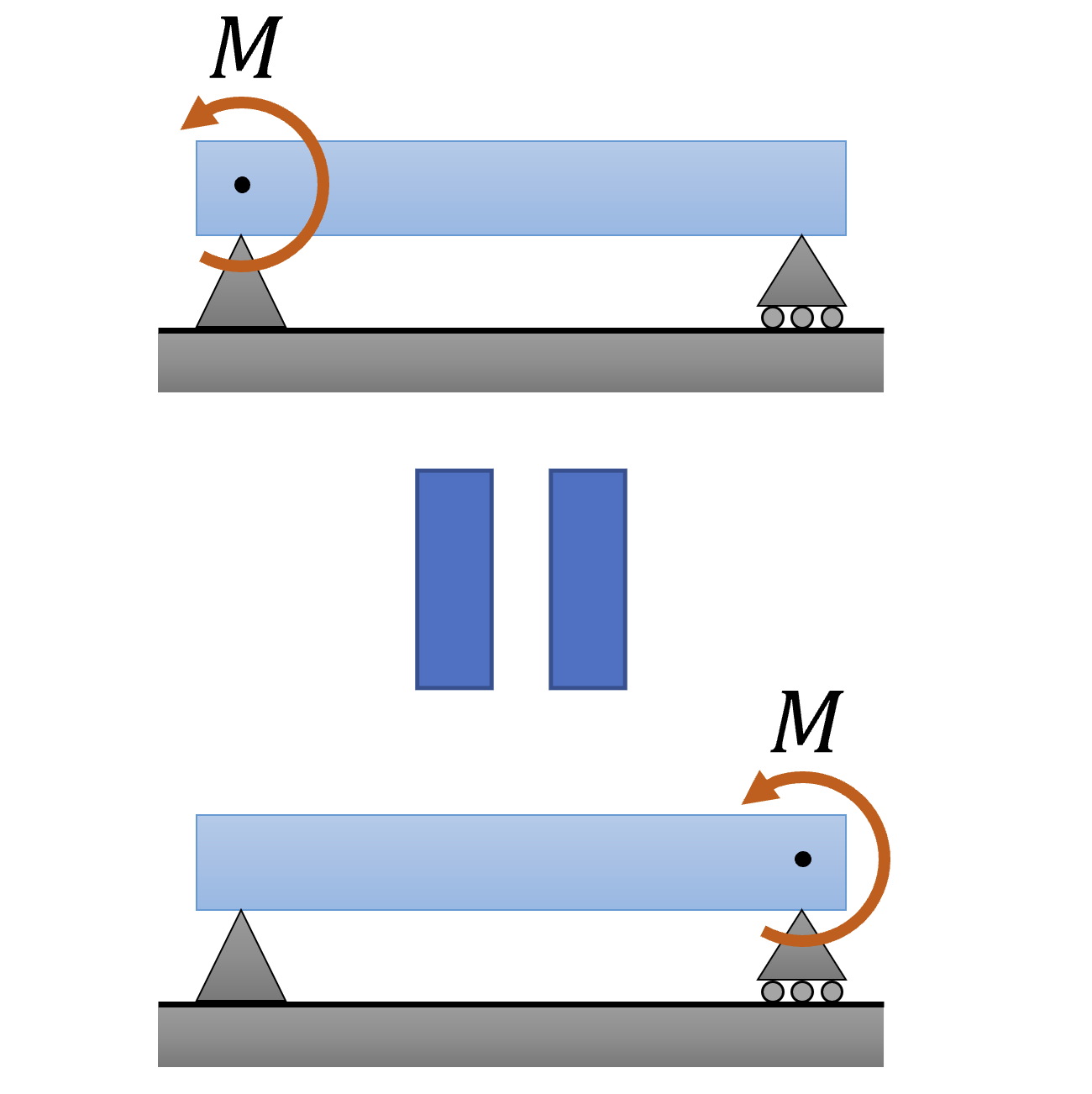
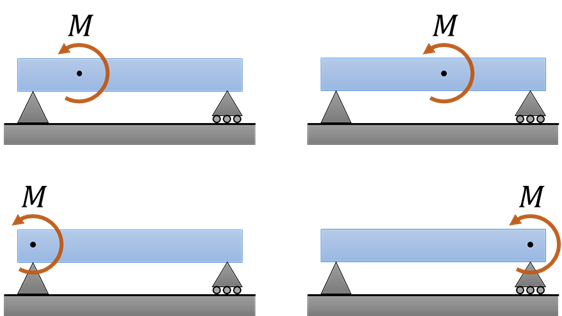
In statics, moments – or couples – are treated as “free vectors” which means that they can move freely unless the direction of application is changed. It implies that the point of application of moment is meaningless while that of force is not. Therefore, the beams shown below are exactly under the same condition as a point of view of statics. (But not of mechanics of materials! It should be carefully treated.) Reactions on supports are equal for all the cases.
But why? How can it be true? Here’s why. Let us consider two forces $F$ acting on a plane and a resultant moment $M$.

If we put the moment vector at the mid-point of two points of application of two forces, just for now, then the point of application of $M$ can move freely in $x$ direction because we can move two $F$s along the line of action of each force.

But the problem is how we can move $M$ in $y$ direction. Here’s how. Place two forces like this.

Then let’s add another two forces, $F_a$s, with same magnitudes, same line of action and opposite directions which change nothing because they cancel out. In terms in statics, the system of forces before and after adding these two forces are equivalent.

If we set the magnitude of $F_a$ correctly, sum of $F$ and $F_a$, $F_r$, can be made to be in $y$ direction.

Now all we have here are two forces, $F_r$s pointing in $y$ or $-y$ direction. We can move the point of application of $M$ freely in $y$ direction just like we did above in $x$ direction. This is why point of application of moment is meaningless and moment vectors are free vectors.
- lazy engineer
'mechanics' 카테고리의 다른 글
| 힘이 축에 대해 가하는 모멘트 계산하기 (0) | 2024.05.10 |
|---|---|
| 타원, 케플러, 궤도운동 (0) | 2024.04.29 |
| [mechanics] Truss analysis: Practice (0) | 2022.08.31 |
| 마찰력의 역학적 이해 (부제: 초원이는 꼭 손을 내밀어야 했을까) (0) | 2022.08.30 |
| [mechanics] Regardlessness of point of moment calculation about an axis (0) | 2022.08.26 |
