티스토리 뷰

(한빛미디어에서 모집하는 혼공학습단 활동의 일환으로 혼자 공부하는 머신러닝+딥러닝 책을 공부하고 작성한 글입니다. 책은 제 돈으로 샀습니다. 본문의 코드는 책의 소스코드를 기반으로 하되 글 흐름에 맞게 수정한 것입니다. 원본 코드는 저자 박해선 님의 깃허브에서 보실 수 있습니다. 책에 나오는 넘파이, 판다스 등의 내용은 본 글에는 자세히 넣지 않았습니다. 본 글의 코드는 제 깃허브에서 보실 수 있습니다.)
5장은 지금까지와 다르게 참 많은 내용이 나옵니다. 대부분은 공식 문서에 굉장히 잘 설명되어 있습니다. 아래는 본 글을 쓰면서 참고한 공식 문서들입니다.
- sklearn.tree.DecisionTreeClassifier
- sklearn.tree.plot_tree
- Decision Trees
- Cross-validation
- Grid Search
- sklearn.model_selection.cross_validate
- sklearn.model_selection.RandomizedSearchCV
- Ensemble methods
아래는 4장 문서에도 올렸던 페가님의 강의 영상입니다. 본 5장과 겹치는 내용이 많아서 문서에 붙입니다.
설명 가능한 알고리즘?
생선이 약간 지루해질 쯤인데 새로운 데이터가 등장했군요. 이번엔 와인 분류입니다. 알코올 도수, 당도, 산도만으로 레드 와인인지 화이트 와인인지 구분하고 싶습니다. 단어가 좀 길군요. 지금부터 알코올 도수는 “도수”, 레드 와인은 “레드”, 화이트 와인은 “화이트”라고 부르겠습니다. 문제를 보니 길이, 두께, 무게 등으로 생선을 분류하는 것과 크게 다르지 않은 것 같습니다. 로지스틱 회귀를 바로 적용해보죠. 우선 데이터를 불러옵니다.

마지막 컬럼 class가 타겟입니다. 레드는 0, 화이트는 1입니다. 데이터를 넘파이 배열로 바꾸고, 훈련/테스트 세트를 나누고, 표준화 전처리를 하고, 사이킷런의 LogisticRegression으로 분류 모델을 만들고 평가까지 합니다.

점수가 좀 낮군요. 과소적합인가 봅니다. 점수를 높이는 건 나중에 생각하고 일단 결과를 출력해봅니다.

그런데… 뭔가 묘한 느낌이 듭니다. 로지스틱 회귀 알고리즘의 동작 개념은 어렵지 않습니다. 계수를 찾아내는 과정도 수학적으로 깔끔합니다. 그래서 나온 이 계수는 도대체 무슨 의미일까요? 도수와 당도와 산도에 왜 0.5와 1.7과 -0.7을 곱하며, 왜 모든 것들의 합에 1.8을 더하면 답이 나올까요? ‘왜’를 설명하자니 좀 어렵습니다. 설명하기에 좋은 다른 방법이 있으면 좋을 것 같습니다.
결정 트리 학습법
아래 그림은 타이타닉호 탑승객의 생존 여부를 트리의 형태로 그려본 것입니다. 탑승객의 성별, 나이, 배우자 또는 자녀 또는 형제/자매의 수에 따라서 각 노드에서 분기하면 최종적으로 생존 확률을 알 수 있습니다. 한때 유행했던 성격 유형 검사 같은걸 떠올리면 됩니다.

위 트리를 보면 몇 가지 사실을 알 수 있습니다.
- 여자이기만 해도 남자에 비해 생존 확률이 두 배 정도로 높았습니다.
- 9.5세 이하의 남자 아이는 전체의 4%밖에 되지 않았습니다. 9.5세 이하이니 배우자는 없었을테고, 형제/자매가 3명 이상이냐 아니냐에 따라서 생존 확률이 엄청나게 차이가 났습니다.
- 그 어디에도 확률 0이나 1은 없으므로 위 트리가 완벽한 답을 내어주지는 않습니다. 사실 모든 머신러닝 알고리즘이 문제를 완벽하게 해결해주지는 못합니다.
이와 같이 특성feature을 하나씩 골라 질문하고 분기하는 방식으로 답을 찾아가는 것이 결정 트리decision tree 학습법입니다.
그럼 단지 설명하기 좋으려고 결정 트리를 쓰느냐? 꼭 그렇지는 않습니다. 결정 트리는 비선형성이 내재된 데이터를 학습할 수 있고, 일반적으로 선형 모델에 비해 정확도가 높다고 알려져 있습니다. 자세한 내용은 여기를 보시면 좋겠습니다. 아래는 페가님의 강의 영상 초반을 캡쳐한 것입니다.

결정 트리는 사이킷런의 DecisionTreeClassifier 클래스를 사용합니다. 결정 트리에는 표준화가 필요하지 않습니다. 선형 회귀와 로지스틱 회귀에서 표준화가 필요했던 이유는, 표준화를 하지 않으면 각 특성의 스케일이 의사결정에 사용하는 어떤 값에 기여하는 정도가 달라지기 때문입니다. k-최근접 이웃 분류에서 표준화를 하지 않았을 때 생선을 무게만으로 분류했던 것을 떠올려보면 됩니다. 결정 트리는 각 단계에서 특성을 하나만 사용하므로 다른 특성의 스케일이 영향을 끼치지 않습니다.

과대적합이군요. 실제로 트리가 어떻게 만들어졌는지를 보면 왜 그런지 힌트를 얻을 수 있습니다. 사이킷런의 plot_tree 함수에 방금 훈련한 DecisionTreeClassifier 모델을 입력으로 넣으면 됩니다.

실로 엄청난 트리가 만들어졌습니다. 시간도 37초나 걸리네요. 코드 셀의 실행 버튼에 마우스를 올려두면 정확한 소요 시간을 알 수 있습니다.

데이터가 맨 처음 만나는 노드를 루트 노트root node, 맨 아래 노드를 리프 노드leaf node라고 부릅니다. 루트 노드의 깊이는 0이며 한 단계 내려갈 때마다 깊이는 1이 추가됩니다. 위 트리는 깊이가 21이나 됩니다. 이렇게 많은 깊이와 노드를 거치는 바람에 훈련 데이터에 과적합이 일어났습니다. 과적합을 줄이는 간단한 방법은 트리의 깊이를 제한하는 것입니다. 깊이를 3으로 줄여서 다시 훈련해보겠습니다. DecisionTreeClassifier의 max_depth 파라미터를 조절하면 됩니다.

훈련/테스트 세트의 점수가 비슷해졌습니다. 트리가 어떻게 생겼는지 다시 보겠습니다.

아까보다 훨씬 심플해졌군요. 여기에 몇 가지 파라미터를 추가하면 더 이해하기 좋은 트리를 볼 수 있습니다. 위 트리에 보이는 X[0], X[1], X[2]는 입력 데이터의 특성을 말합니다. feature_name을 설정하면 이것을 실제 특성인 도수, 당도, 산도로 바꿀 수 있습니다. filled를 True로 설정하면 클래스의 순도를 색깔로 표시할 수 있습니다.

각 노드를 보면 당도, 도수, 산도로 와인을 분류한 것을 볼 수 있습니다. 루트 노드를 보니 당도 4.325를 기준으로 나누는군요. 그 아래 값을 보면 알겠지만 답이 True이면 왼쪽으로, False이면 오른쪽으로 갑니다. 노드마다 그 노드에 도착한 샘플 총 개수와 각 클래스의 샘플 개수가 나옵니다. value=[100, 200]는 해당 노드에 레드(0) 100개, 화이트(1) 200개가 도착했음을 뜻합니다. 레드의 순도가 높을수록 파란색이 진해지고 화이트의 순도가 높을수록 주황색이 진해지는 것도 볼 수 있습니다.
책에는 나오지 않지만 과적합을 해결하는 한 가지 방법이 더 있습니다. 과적합이 일어나는 이유 중 하나로, 샘플이 단 두 개만 남아있어도 기어이 하나씩 분류하는 것이 있습니다. 리프 노드의 최소 샘플 개수를 조절하면 됩니다. DecisionTreeClassifier의 min_samples_leaf 파라미터입니다.

깊이를 늘렸는데 점수가 약간 올라간 게 보이는군요.
그럼 트리를 만드는 방법과 보는 방법은 대충 알 것 같습니다. 한 가지만 빼고요. gini란 뭘까요? 트리는 무엇을 최대화 또는 최소화할까요?
지니 불순도
gini는 지니 불순도nini impurity를 뜻합니다. 계산 방법은 간단합니다.
$gini = {1 - \left( { ratio_{class0} } \right )^2-\left( { ratio_{class1} } \right )^2 }$
현재 분류된 결과를 보면 루트 노드의 지니 불순도는
$gini = {1-\left({{1258}\over{5197}}\right)^2-\left({{3939}\over{5197}}\right)^2}=0.367$
입니다. 순도가 가장 높을 때에는 한 클래스의 샘플만 있으므로 지니 불순도가 0임을, 최악의 경우에는 두 클래스가 동수로 있으므로 지니 불순도가 0.5임을 알 수 있습니다. 즉, 지니 불순도는 $[0, 0.5]$ 범위의 값을 가질 수 있습니다.
결정 트리는 부모 노드와 자식 노드의 불순도 차이가 가능한 커지도록 데이터 분할 기준을 잡습니다. 부모 노드와 자식 노드의 불순도 차이를 정보 이득information gain이라고 부릅니다. 계산식은 아래와 같습니다.
$(gini_{parent})
- {(no.\:samples_{left}) \over (no.\:samples_{parent})} \times (gini_{left})
- {(no.\:samples_{right}) \over (no.\:samples_{parent})} \times (gini_{right})$
결정 트리가 불순도 차이를 계산하는 방법은 한 가지 더 있습니다. DecisionTreeClassifier에는 criterion 파라미터가 있는데, 이걸 기본값인 ‘gini’로 두면 위의 정보 이득을 기준으로 샘플을 나눕니다. 이걸 ‘entropy’로 두면 아래의 엔트로피 불순도를 이용합니다.
$-(ratio_{class\:0})\times log_{2}(ratio_{class\:0})-(ratio_{class\:1})\times log_{2}(ratio_{class\:1})$
결정 트리로 샘플을 분류할 때 어느 특성이 가장 중요하게 작용했는지를 볼 수 있습니다. DecisionTreeClassifier의 feature_importances_ 값을 보면 됩니다.

1번 특성인 당도의 중요도가 가장 높았다고 하는군요. 실제로 트리를 보면 모든 데이터가 통과하는 깊이 0과 1이 모두 당도를 기준으로 분류한 걸 볼 수 있습니다.
교차 검증
이제 조금 다른 얘기를 해보고자 합니다. 지금까지 전체 데이터를 훈련 데이터와 테스트 데이터로 나눴습니다. 그리고 매번 비슷한 패턴이었습니다.
- 일단 적당한 파라미터로 학습을 시켜본다.
- 훈련/테스트 데이터의 점수가 둘이 비슷하게 높도록 파라미터를 수정한다.
그런데 생각해보니 이 방식도 조금 이상합니다. 결국 매번 같은 데이터로 학습하는 거잖아요? 이래서는 테스트 데이터를 나누는 의미가 퇴색될 것 같습니다. 아래처럼 방식을 바꾸면 어떨까요?
- 전체의 60%를 훈련 세트로 만들고 모델을 만들거나 수정한다.
- 전체의 20%를 검증 세트로 만들고 모델이 수정될 때마다 검증한다.
- 나머지 20%를 테스트 세트로 만들고 최종 확인용으로 한 번만 사용한다.
이런 방식이 더 확실한 검증 및 테스트가 될 것 같습니다. 물론 60%, 20%, 20%의 비율은 달라질 수 있습니다. 이왕이면 검증 세트도 한 번 만들고 끝내는 게 아니라 서로 다르게 여러 번 만들면 어떨까요? 아래처럼 말이죠.

이런 방식의 검증을 교차 검증cross validation이라고 부릅니다. 특히 k개의 세트로 나누고 검증 세트를 바꿔가며 검증하는 것을 k-폴드 교차 검증이라고 부릅니다.
훈련 세트를 세 부분으로 나눠서 교차 검증을 수행하는 것을 3-폴드 교차 검증이라고 합니다. 통칭 k-폴드 교차 검증(k-fold cross validation)이라고 하며, 훈련 세트를 몇 부분으로 나누냐에 따라 다르게 부릅니다. k-겹 교차 검증이라고도 부릅니다.
박해선, 혼자 공부하는 머신러닝 + 딥러닝, 한빛미디어, 245쪽
교차 검증을 굳이 반복문으로 짜라면 짤 수도 있겠지만, 그럴 필요가 없습니다. 사이킷런이 이미 다 준비해뒀거든요. cross_validate()라는 함수입니다.

교재에는 fit()을 마친 dt를 cross_validate()에 전달하는 것처럼 되어 있지만, 어차피 cross_validate가 알아야 할 것은 fit의 결과가 아니라 모델 그 자체이므로 DecisionTreeClassifier 객체만 전달해도 됩니다.
cross_validate의 입력 파라미터 중 cv가 있는데, 이걸로 훈련/검증 세트를 어떻게 나눌지를 정할 수 있습니다. 이걸 분할기splitter라고 부릅니다.
사이킷런의 분할기는 교차 검증에서 폴드를 어떻게 나눌지 결정해 줍니다. cross_validate() 함수는 기본적으로 회귀 모델일 경우 KFold 분할기를 사용하고 분류 모델일 경우 타깃 클레스를 골고루 나누기 위해 StratifiedKFold를 사용합니다.
박해선, 혼자 공부하는 머신러닝 + 딥러닝, 한빛미디어, 247쪽
cv의 기본값은 None이며 이 경우 5-폴드 교차 검증을 진행합니다. 10-폴드 교차 검증을 하려면 아래와 같이 코드를 작성합니다.

하이퍼파라미터 튜닝
하이퍼파라미터는 모델이 학습해줄 수 없는 파라미터를 말합니다. 릿지/라쏘 회귀에서의 $alpah$, 미니배치 학습에서 배치의 크기 등이 하이퍼 파라미터에 해당됩니다. 그래서 사람이 직접 값을 찾아야 했죠. 하지만 이것도 이왕이면 알고리즘이 알아서 찾아주면 좋을 것 같습니다. 사이킷런의 그리드 서치Grid Search가 이 작업을 위한 도구입니다. 정말 사이킷런은 다 준비해뒀군요. 사랑해요 사이킷런!
GridSearchCV는 이름 뒤에 CV가 붙어있듯이 교차 검증까지 한방에 해줍니다. 아래 코드는 결정 트리에서 불순도가 어느 값 이상으로 낮아지지 않으면 더 깊이 들어가지 않도록 제한하는 코드입니다. DecisionTreeClassifier의 min_impurity_decrease 파라미터가 이 역할을 담당합니다. GridSearchCV.fit()은 전달된 모델, 파라미터 등을 이용하여 교차 검증까지 진행합니다. 바로 훈련까지 해보죠.
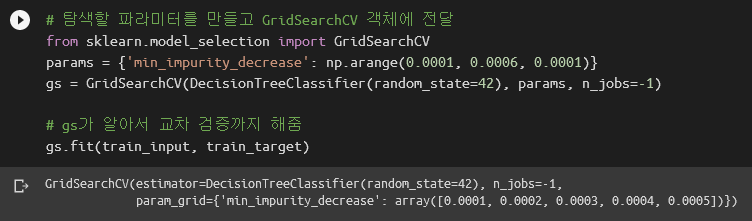
n_jobs는 병렬 계산에 사용할 CPU 코어 개수를 지정합니다. 기본값은 1이며 -1로 두면 시스템에 있는 모든 코어를 사용합니다. 이렇게 만들어진 gs 객체에는 최고 점수를 보인 모델, 파라미터, 교차 검증 점수가 모두 들어있습니다. 완전 쩌네요.

그리드 서치의 진짜 놀라운 점은 이게 아닙니다. 위 예제는 파라미터가 min_impurity_decrease 하나였습니다. 파라미터가 하나여야 할 이유는 없죠. 그리드 서치라는 이름에 어울리게 여러 개의 파라미터에 대해서 모든 조합을 검사할 수 있어야 합니다. 아래는 min_impurity_decrease, max_depth, min_samples_split, 총 3개의 파라미터에 대해 그리드 서치를 수행하는 코드입니다. min_samples_split은 트리의 노드에서 데이터를 분할할 수 있는 최소 샘플 개수입니다.
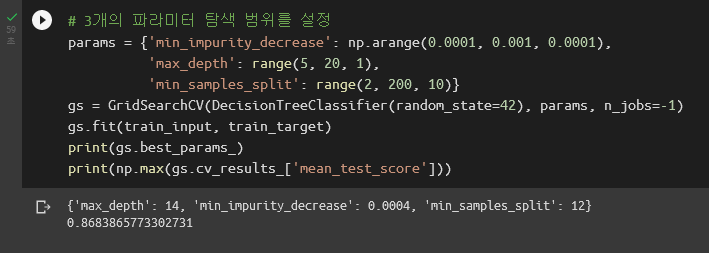
총 1350개의 케이스 각각에 대해 5-폴드 교차 검증을 돌리느라 시간이 꽤 걸리는군요. 저는 59초 걸렸습니다.
랜덤 서치
최적화를 공부해본 분들이라면 그리드 서치를 보자마자 이런 생각이 떠오를 겁니다. 아니, 떠올라야 합니다.
그리드 서치는 그냥 브루트 포스brute force잖아.
시간만 있음 누가 못해.
좀 더 그럴싸한 전략이 있어야 하지 않나?
즉 하이퍼파라미터에 대한 최적화 문제를 만들면 어떨까 하는 것이죠. 그런데 이런 방식은 문제가 너무 커지는 감이 있습니다. 이미 머신러닝이 최적화 문제인데, 최적화 문제의 하이퍼파라미터를 또 최적화 하다니? 그럼 아쉬운 대로 다른 전략을 이용해보죠. 격자점을 만들어서 그리드 서치를 하는게 아니라, 파라미터의 범위만 주고 랜덤하게 샘플링 하는 겁니다. 예를 들어 아래처럼 4개의 파라미터의 범위만 주고,

4차원 공간에서 랜덤하게 100개의 파라미터 조합을 뽑아서 훈련 시켜보는거죠.

점수는 그리드 서치와 별 차이가 없습니다. 하지만 시간이 훨씬 적게 소요됐죠. 그래도 조심할 점은 있습니다. 랜덤 서치는 그리드 서치보다 오히려 더 나쁜 파라미터를 찾아줄 가능성도 있습니다. 그리드 서치는 모든 격자점을 촘촘하게 다 검사하는 반면, 랜덤 서치는 추출된 점이 어디에 어떻게 분포될지 알 수 없습니다. 운이 나쁘면 성능이 좋지 않은 한 곳에 몰려있을 수도 있으니까요. 그리드 서치와 랜덤 서치를 적절히 섞어서 사용하면 어떨까 하고 생각해봅니다. 써놓고 보니 뒤이어 나올 앙상블과도 연결이 될 것 같군요.
트리의 앙상블
앙상블은 이름에서 알 수 있듯이 여러 모델을 합쳐서 하나의 모델을 만드는 것을 말합니다. 이 방식으로 단일 모델에 비해 일반화 성능generalizability과 강인성robustness을 향상시킬 수 있다고 하는군요. 원래 통계에서 말하는 앙상블은 동일한 이벤트를 여러 번 수행하여 그 결과를 보는 것을 말하는데, 머신러닝에서도 비슷한 개념으로 차용했다고 볼 수도 있겠네요. 앙상블은 크게 두 가지가 있습니다. 평균화averaging method와 부스팅boosting method입니다. 경우에 따라 스태킹stacking을 포함하여 세 가지로 보기도 하는 모양입니다.
평균화에는 배깅bagging, 랜덤 포레스트random forest, 엑스트라 트리extra tree 등이 있습니다. 구글링을 해보면 앙상블을 배깅과 부스팅으로 분류하기도 합니다. 일단 저는 사이킷런 공식 문서를 따르겠습니다. 평균화는 예측기estimator 여러 개를 만들고 각 예측기의 예측을 평균하여 하나의 예측을 추출하는 방법입니다. 개별 예측기는 분산이 크지만 평균화를 통해 분산을 줄일 수 있습니다.
배깅은 bootstrapping aggregating의 약자로 과대적합을 방지하는 방법 중 하나입니다. 부트스트랩 샘플링bootstrap sampling은 샘플을 뽑되 중복을 허용하는with replacement 것을 말합니다. 예를 들어 훈련 세트에 100개의 샘플이 있다면 중복을 허용하여 100개를 뽑아 새로운 샘플을 만듭니다. 이렇게 만들어진 샘플을 부트스트랩 샘플이라고 부릅니다. 당연히 이 안에는 중복된 샘플이 들어있을 것이고 원본의 데이터를 대표하지 못합니다. 대신 각 샘플은 이전 샘플에 대해 독립성을 갖습니다. 이제 각 샘플에 대해서 모델을 구성하고, 분류 문제일 경우 각 모델의 결과를 보팅voting, 회귀 문제일 경우 평균하여 결과를 도출합니다. 사이킷런에서는 sklearn.ensemble.BaggingClassifier와 sklearn.ensemble.BaggingRegressor를 사용합니다.

랜덤 포레스트random forest는 랜덤하게 만들어진 트리 여러 개로 이루어진 숲forest을 만드는 방식입니다. 각 트리가 학습하는 데이터는 앞에서 말한 부트스트랩 샘플입니다. 여기에 한 가지 무작위성을 추가합니다. 각 노드에서 데이터를 분할할 때 특성을 모두 사용하지 않고 일부만 사용합니다. 정확히는 전체 특성 개수의 제곱근만큼의 특성만을 사용합니다. 전체 특성이 4개라면 그 중 2개를 랜덤으로 골라서 쓰는 거죠. 이 작업을 모든 노드에서 수행합니다. 이렇게 의도적으로 무작위성을 넣는 이유는, 이렇게 하지 않으면 트리는 쉽게 과대적합이 되기 때문입니다. 미드 빅뱅이론에 비유하자면 너무 잘나서 본인이 정한 정답 이외에는 모두 오답처리해버리는 쉘든 1명보다, 약간 부족한 듯한 레너드와 하워드와 라지와 페니를 합쳐서 모델을 만드는 겁니다. 사이킷런에서는 sklearn.ensemble.RandomForestClassifier와 sklearn.ensemble.RandomForestClassifier를 사용합니다.

RandomForestClassifier에는 재밌는 기능이 있습니다. 부트스트랩 샘플링 과정 중에 선택받지 못한 샘플을 모아서 모델을 검증할 수 있습니다. 이런 샘플을 OOB(Out-Of-Bag)라고 부른다는군요. OOB 점수를 보기 위해서는 RandomForestClassifier 객체를 만들 때 oob_score를 True로 설정해야 합니다.

엑스트라 트리extra tree는 이름만으로 오해를 사기에 딱 좋습니다. 여기서 엑스트라는 깍두기라는 의미의 엑스트라가 아니고 EXTremely RAndomized Tree를 의미합니다. 도대체 얼마나 무작위성을 넣기에 극단적으로extremely 랜덤하다고 할까요? 여기서는 각 노드에서 분할 기준을 아예 무작위로 잡아버립니다. 어떤 노드에서 사용할 특성을 와인의 산도와 당도로 결정했다면, 가장 좋은 성능의 분할 기준을 정하는게 아니라 랜덤 산도와 랜덤 당도가 분할 기준 후보가 됩니다. 그리고 둘 중 그나마 나은 걸 최종 분할 기준으로 정합니다. 그래서 각 트리의 성능은 매우 떨어질 수밖에 없습니다. 대신 랜덤하게 기준을 정하므로 매우 빨리 트리를 생성할 수 있습니다. 엑스트라 트리는 기본적으로 랜덤 포레스트처럼 많은 트리를 만들어서 평균을 하므로 과대적합을 방지하고 일반화 성능이 높아지는 효과가 있습니다. 엑스트라 트리는 사이킷런의 sklearn.ensemble.ExtraTreesClassifier와 sklearn.ensemble.ExtraTressRegressor를 사용합니다.

기본 미션: 교차 검증을 그림으로 설명하기

그레디언드 부스팅과 히스토그램 기반 그레디언트 부스팅은 추후 업데이트 하겠습니다.
공부에 도움 주신 코봉님, 정도전님, 페가님께 감사 말씀 드립니다.
'혼공머신' 카테고리의 다른 글
| [혼공머신] 7장. 딥러닝을 시작합니다 (2) | 2022.08.21 |
|---|---|
| [혼공머신] 6장. 비지도 학습: 비슷한 과일끼리 모으자! (0) | 2022.08.14 |
| [혼공머신] 4장. 다양한 분류 알고리즘: 럭키백의 확률을 계산하라! (0) | 2022.07.24 |
| [혼공머신] 3장. 회귀 알고리즘: 농어의 무게를 예측하라! (0) | 2022.07.17 |
| [혼공머신] 2장. 데이터 다루기: 수상한 생선을 조심하라! (0) | 2022.07.10 |
