티스토리 뷰
(한빛미디어에서 모집하는 혼공학습단 활동의 일환으로 혼자 공부하는 머신러닝+딥러닝 책을 공부하고 작성한 글입니다. 책은 제 돈으로 샀습니다. 본문의 코드는 책의 소스코드를 기반으로 하되 글 흐름에 맞게 수정한 것입니다. 원본 코드는 저자 박해선 님의 깃허브에서 보실 수 있습니다. 책에 나오는 넘파이, 판다스 등의 내용은 본 글에는 자세히 넣지 않았습니다. 본 글의 코드는 제 깃허브에서 보실 수 있습니다.)
목차
4. 확률적 경사 하강법: 분류 모델의 계수를 찾는 방법
8. 기본 미션: 04-1 확인 문제 2번 풀이과정 설명
9. 선택 미션: 04-2 과대적합/과소적합 코랩 화면 캡쳐
1. 분류의 정확도
2장의 분류 문제를 다시 보겠습니다. 도미와 빙어의 길이 및 무게 데이터를 KNeighborsClassifier에게 모두 알려준 후, 새로운 생선이 들어오면 길이와 무게로부터 도미인지 빙어인지 분류하는 문제였습니다. 분류 기준은 가까이에 어떤 생선이 주로 있는지였습니다. 아래는 해당 코드입니다. 데이터 전체를 또 쓰기가 번거로워서 데이터를 구글 드라이브에 저장한 후 코랩으로 불러왔습니다. 방법은 여러 가지가 있습니다. 원래는 저자 분의 깃허브 링크에서 데이터를 바로 가져오고 싶었는데 깔끔한 방법을 찾지 못했습니다. (requests로 가져와서 eval 하는 것은 제가 원하는 방법이 아닙니다. 저는 eval을 싫어합니다.) 좋은 방법을 아시는 분은 알려주세요!
데이터를 확인합니다.
여기에 일부러 길이와 무게가 어중간한 생선을 넣어보겠습니다.
오호, 도미로 분류되었군요. 가까운 5개 중 3개가 도미, 2개가 빙어입니다. 어쨌든 3>2니까 도미이긴 한데… 결과도 참 어중간합니다. 그럼 이 생선은 도미일 확률이 60%, 빙어일 확률이 40%라고 얘기해도 될까요? 그 확률을 보여주는 메서드가 있습니다. predict_proba()입니다.
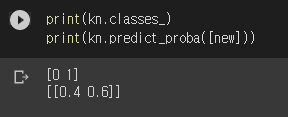
빙어(0)일 확률 40%, 도미(1)일 확률 60%로 판단했군요. 그런데 이런 방식이라면 확률은 이산 값이 됩니다. 확률은 연속이어야 맞지 않을까요? 여기에 적용할 수 있는 것이 로지스틱 회귀입니다.
로지스틱 회귀를 설명하기 전에 새로운 데이터를 준비합니다. 생선은 총 7총으로 bream, roach, whitefish, parkki, perch, pike, smelt입니다. 각각의 한글명을 찾고 싶었는데 나오지 않네요. 원문 그대로 쓰겠습니다. 각 생선 개체마다 무게, 길이, 대각선 길이, 높이, 두께를 준비했습니다.
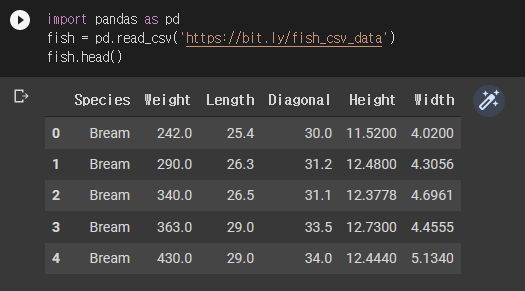
오른쪽의 요술봉을 누르니 UI가 인터랙티브하게 바뀌네요. 놀랍! 중요한 건 아니니 넘어갑니다. Species가 타겟이 되고 Weight부터 Width까지는 입력 데이터입니다. 데이터를 준비하고 훈련/테스트 세트로 나누고 표준화 전처리를 합니다.
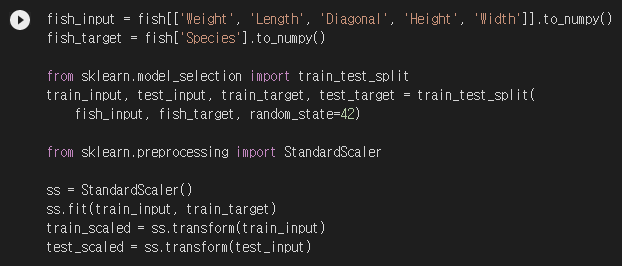
데이터 준비가 완료되었습니다. 본격적으로 로지스틱 회귀로 들어가보겠습니다.
2. 로지스틱 회귀 – 이진 분류
로지스틱 회귀logistic regression는 이름에 회귀가 들어가지만 사실 분류 모델입니다. 누가 네이밍을 이렇게 했는지 모르겠습니다만, 어쩌겠습니까. 따라야죠. 분류 모델이므로 입출력 방식은 k-최근접 이웃 분류와 비슷합니다. 생선의 데이터와 정답을 전부 알려주고, 새로운 데이터가 들어오면 어떤 생선인지 분류합니다. 실제 동작방식은 k-최근접 이웃과 많이 다릅니다. k-최근접 이웃 분류는 새로운 데이터와 훈련 데이터 간의 거리를 이용했습니다. 로지스틱 회귀는 아래 형태의 식에 들어갈 계수를 찾아내는 게 목표입니다.
\begin{align*} z \; = \; &a\times(Weight) \\+ &b\times(Length) \\+&c\times(Diagonal) \\+&d\times (Height) \\+&e\times(Width) \\+&f\end{align*}
계수에는 임의의 실수가 들어갈 수 있으므로 $z$ 값의 범위는 $(-\infty, \infty)$입니다. 이걸 확률로 바꾸는 함수가 필요합니다. 그 이름도 유명한 시그모이드 함수sigmoid function입니다. 로지스틱 함수logistic function라고도 부릅니다. 이 함수는 뒤에 신경망에서 굉장히 중요한 역할을 하게 됩니다.
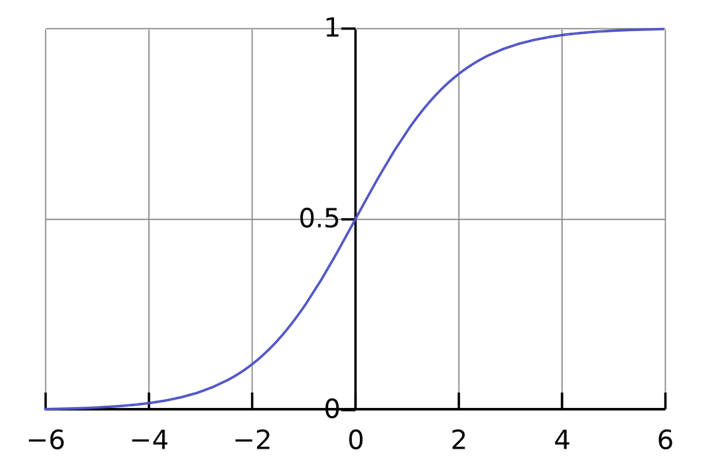
시그모이드 함수는 아래와 같습니다.
$\phi(z) = {1 \over {1 + e^{-z}}}$
시그모이드는 임의의 실수에 대해서 $(0, 1)$ 범위의 값을 뱉어내므로 확률처럼 다룰 수 있습니다. 그럼 확률은 이걸로 만든다 치고, 각 특성에 곱할 계수는 뭘 기준으로 찾을까요? 수식 없이 개념적으로만 설명하자면, “정답의 확률은 최대한 높게, 오답의 확률은 최대한 낮게” 만드는 방향으로 계수를 찾습니다. 말이 좀 어려울 수 있으니, 일단 코드를 돌려보고 값을 이용해서 설명해보겠습니다. 우선 도미와 빙어만 분류하는 이진 분류입니다.
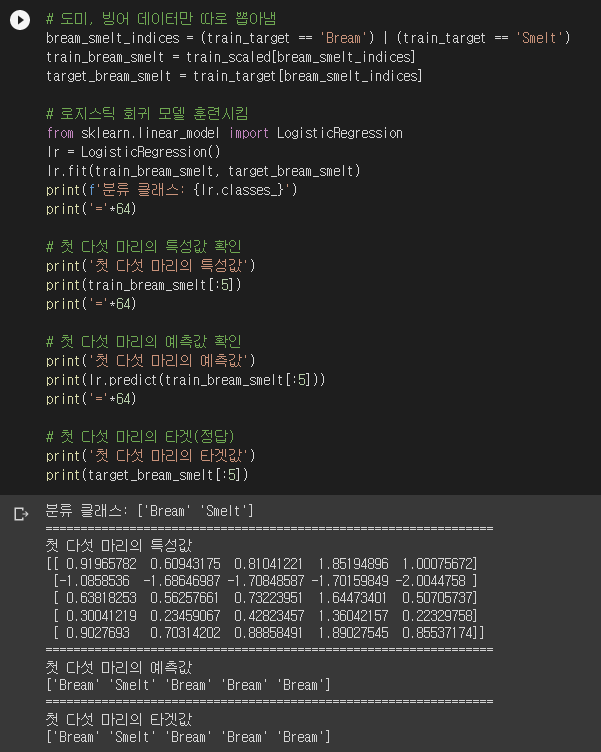
로지스틱 회귀는 사이킷런의 LogisticRegression 클래스를 사용합니다. LogisticRegression의 classes_ 속성에는 분류 클래스가 순서대로 들어있습니다. Bream이 0이고 Smelt가 1입니다. 첫 다섯 마리를 순서대로 도미, 빙어, 도미, 도미, 도미로 예측했습니다. LogisticRegression이 찾아낸 계수는 lr.coef_와 lr.intercept_에 들어있습니다.
따라서 모델이 찾아낸 식은 아래와 같습니다.
\begin{align*} z = &- 0.404\times(Weight) \\ &- 0.576\times(Length) \\ &- 0.663\times(Diagonal) \\ &- 1.013\times (Height) \\ &- 0.732\times(Width) \\ &- 2.162 \end{align*}
계수가 전부 음수네요? 다 이유가 있습니다. 잠시 뒤에 설명하겠습니다. 특성치를 이 식에 대입한 $z$ 값은 decision_function() 메서드를 이용하면 볼 수 있습니다.
$z$ 값은 2번만 양수이고 나머지는 음수군요. 이걸 시그모이드에 넣으면? 시그모이드는 사이파이의 expit()를 사용합니다.
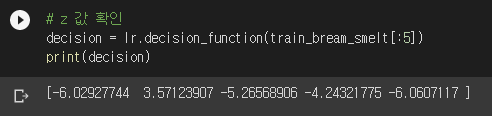
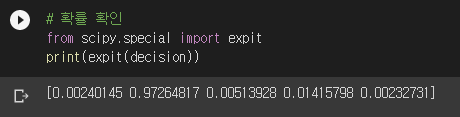
예측값과 타겟값은 [도미, 빙어, 도미, 도미, 도미]였습니다. 시그모이드 계산 결과는 [0, 1, 0, 0, 0]에 근접하군요. 도미가 0이고 빙어가 1이므로 일치하는 결과가 나왔습니다. 즉, 로지스틱 회귀는 시그모이드 함수값이 정답인 [0, 1, 0, 0, 0]에 최대한 가까이 나오도록 계수를 찾습니다. “정답의 확률은 최대한 높게, 오답의 확률은 최대한 낮게”의 의미가 바로 이것입니다. 시그모이드는 $z$ 값이 작을수록 0에, 클수록 1에 가까워집니다. 따라서 도미의 $z$ 값은 최대한 작게, 빙어의 $z$ 값은 최대한 크게 나와야 합니다. 첫 다섯 마리의 특성값이 어떻게 생겼었냐면,
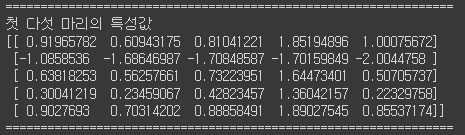
이렇게 생겼습니다. 왜 계수가 전부 음수인지 아시겠죠? 사실 LogisticRegression에는 확률값을 알려주는 메서드가 있습니다. predict_proba()입니다.
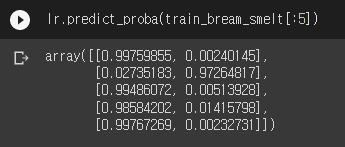
시그모이드를 직접 계산한 것과 정확히 일치하는 값이 나오네요.
3. 로지스틱 회귀 – 다중 분류
좀 전에 한 것은 클래스가 2개 뿐인 이진 분류binary classification입니다. 클래스가 3개 이상인 분류를 다중 분류multiclass classification라고 부릅니다. 원래의 데이터는 생선이 총 7종이었습니다. 새로운 생선이 들어왔을 때 7종 각각에 대한 확률을 계산하려면 시그모이드가 아닌 다른 함수를 써야 합니다. 역시 그 유명한 소프트맥스 함수softmax function입니다.
$e(z)_i = {{e^{z_i} \over {\sum_{j=1}^{K} e^{z_j}}}}$
LogisticRegression은 분류 클래스의 개수에 따라 시그모이드를 쓸지 소프트맥스를 쓸지 알아서 정해줍니다. 공식 문서에 나와있는 내용입니다. 소프트맥스가 어떻게 적용되는지를 이해하려면 먼저 모델이 만들어내는 계수의 구조를 알아야 합니다. 일단 코드부터 돌리고 보겠습니다.
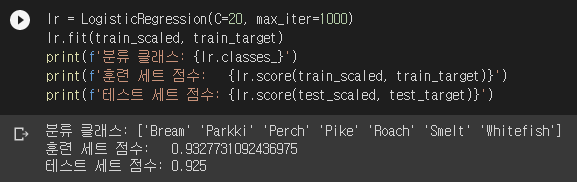
C는 규제의 강도를 결정합니다. LogisticRegression은 무엇을 규제할지 정할 수 있는데 기본은 L2 규제입니다. L1을 규제할 수도 있고, L1와 L2를 함께 규제할 수도 있습니다. 자세한 내용은 공식 문서에 잘 나와있습니다. C는 선형 회귀의 alpha와 반대로 값이 클수록 규제가 약합니다. LogisticRegression은 계수를 찾을 때 반복 알고리즘을 사용합니다. max_iter의 값으로 최대 몇 번까지 반복할 지 정할 수 있습니다.
훈련이 끝났으니 첫 다섯 마리를 제대로 예측했는지 확인해봅시다.
앗… 한 마리가 삑사리가 났군요. 어쩔 수 없죠. 애초에 점수가 100점이 아니었으니까요. 이번엔 계수가 어떻게 생겼는지 보겠습니다.
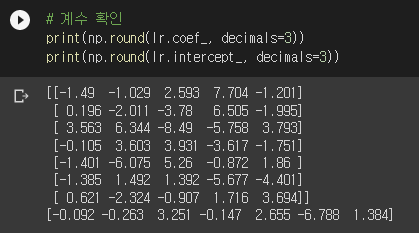
뭐가 엄청나게 많네요. 자세히 보니 coef_의 크기가 (7, 5)입니다. 따라서 coef_의 각 row가 각 생선 종류를 담당함을 알 수 있습니다. 즉, lr.coef_의 각 row와 0번 생선의 특성값을 내적하고 lr.intercept_를 더하면 0번 생선의 각 생선 종류에 대한 z 값이 나옵니다.
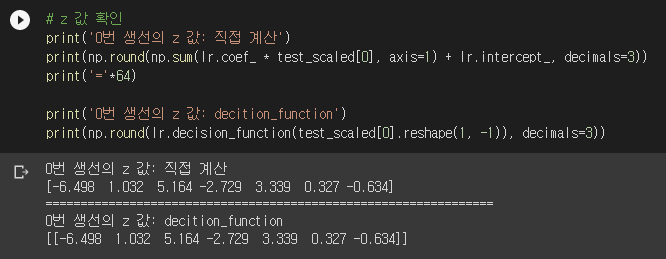
이제 생선 개체마다 z 값이 7개가 나옵니다. 이걸 소프트맥스 함수에 넣으면 확률이 계산됩니다. 확률은 predict_proba() 메서드가 계산해줍니다.
결과의 각 row가 생선 개체이고 각 column이 생선 종류의 확률입니다. 4번째 생선 개체가 다른 것들에 비해 확률이 덜 분명하네요. 타겟은 Whitefish였는데 예측을 Roach로 했던 바로 그 녀석입니다. 이 값은 직접 계산할 수도 있습니다. 사이파이의 softmax()를 사용하면 됩니다.
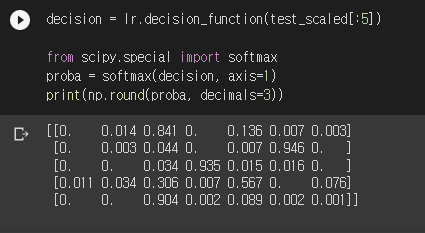
로지스틱 회귀가 계수를 결정하는 기준이 “정답의 확률은 최대한 높게, 오답의 확률은 최대한 낮게”라고 말씀드렸는데요. 사실 이 부분은 엄밀하게 파고 들어가면 얘기할 거리가 많습니다. 이건 나중에 따로 정리해보겠습니다. 일단 좋은 자료를 하나 공유합니다.
당장 중요한 얘기는 아닐 수 있는데, LogisticRegression의 solver를 지정할 수 있습니다. lbfgs, newton-cg, liblinear, sag, saga 등이 있으며 기본값은 lbfgs입니다. bfgs는 최적화를 공부하면 알게 되는 녀석인데 lbfgs의 l은 limited-memory라고 하네요. 음... 뭔지 잘 모르겠으니 나중에 따로 공부해서 올리겠습니다.
4. 확률적 경사 하강법: 분류 모델의 계수를 찾는 방법
로지스틱 회귀는 기본적으로 최적화 문제입니다. 따라서 최적해의 방향을 탐색해가며 조금씩 최적해를 향해 반복적iterative으로 전진해가는 방식을 사용합니다. 산을 내려가는 것으로 비유를 많이 하죠. 로지스틱 회귀의 최적해란 앞서 말한대로 “정답의 확률은 최대한 높게, 오답의 확률은 최대한 낮게” 만들어주는 계수 $w$와 절편 $b$입니다. LogisticRegression의 coef_와 intercept_가 각각 계수와 절편입니다.
훈련 세트가 최초 한번 만들어진 후 바뀌지 않는다면 지금까지 했던 방법을 쓰면 됩니다. 그런데 세상이 그렇게 호락호락한 게 아니죠. 머신러닝의 경우 데이터는 계속해서 추가될 가능성이 높습니다. 그럴 때마다 전체 데이터를 다시 훈련시키려면 리소스가 많이 필요할 겁니다.
이때 필요한 것이 확률적 경사 하강법Stocastic Gradient Descent입니다. 줄여서 SGD라고도 부릅니다. 저는 대학원 때 최적화 이론 수업을 들었어서 경사 하강법Gradient Descent은 알고 있었는데, 확률적 경사 하강법은 이번 기회에 처음 알게 되었네요. 아래는 경사 하강법을 애니메이션으로 만든 영상입니다. 확률적 경사 하강법도 비슷한 애니메이션이 있으면 좋았을텐데 찾지는 못했습니다. 기회가 되면 만들어보도록 하겠습니다.
SGD의 이름에 들어있는 ‘확률적’이라 함은 샘플을 랜덤하게 고른다는 뜻입니다. SGD에서는 훈련 세트에서 샘플을 하나씩 꺼내서 최적해를 찾아갑니다. 각 샘플을 이용해서 현재 위치에서 기울기를 계산하고 $w$와 $b$를 업데이트 합니다. 전체 샘플을 한번씩 사용해서 모델을 훈련시키는 것을 “1 에포크”라고 부릅니다. 뒤에 나오겠지만 모델을 훈련 시키는 데에 100 에포크 넘게 사용할 수 있습니다. 그 이유는 아주 조금씩 전진하기 때문입니다. 스텝의 크기가 커지면 오히려 수렴이 느려지거나 엉뚱한 해를 찾을 수 있습니다.
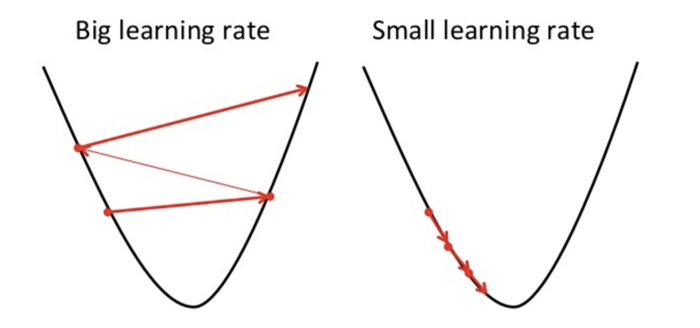
훈련 세트에서 샘플을 하나씩 꺼내서 최적해의 방향을 찾아가야 합니다. 그런데 최적해가 어디에 있는지 모릅니다. 알면 문제를 풀 필요도 없죠. 그래서 현재 위치($w$와 $b$)에서 경사gradient의 방향으로 가면 정확하지는 않아도 어쨌든 비슷하게는 가지 않을까 하고 움직입니다. 경사를 계산하려면 미분가능한 함수가 필요합니다. 여기에 손실 함수loss function의 개념이 등장합니다.
5. 손실 함수: 분류 모델의 목적 함수
분류의 이상적인 상황은 훈련 세트와 테스트 세트의 정확도가 모두 100%가 나오는 것입니다. 최적화 문제는 어떠한 목적 함수를 정의하고 목적 함수를 최소화하는 파라미터를 찾는 것으로 표준화되어 있습니다. 그렇다면 분류의 정확도의 역수나 –(정확도)를 목적 함수로 쓰면 될까 싶은데… 문제가 있습니다. 정확도는 이산적인 값밖에 가질 수 없습니다. 세트의 샘플 개수가 100개라면 정확도는 1% 간격입니다. 따라서 미분을 할 수 없습니다. 평균 변화율이야 어거지로 계산할 수는 있겠지만 우리가 원하는 아름다운 모습은 아닙니다. 그래서 손실 함수를 아래와 같이 정의합니다.
$L(\hat{y}, y) = - (y log\hat{y} + (1-y) log(1-\hat{y}))$
위 식은 이진 분류에 사용하는 손실 함수로, 로지스틱 손실 함수logistic loss function 또는 이진 크로스 엔트로피 손실 함수binary cross-entropy function라고 부릅니다. 식에서 $y$는 타겟이고 $\hat{y}$는 예측값입니다. 위 식은 아래와 같이 동작합니다.
- 타겟이 1일 경우 두 번째 항은 0이 되므로 첫 번째 항만 계산하면 됩니다. 예측값이 1에 가까워야 손실 함수가 작습니다. 예측값이 0에 가까울수록 손실 함수는 증가합니다. 로그를 취하면 예측값이 1에서 멀어질수록 손실 함수에 일종의 페널티가 가해집니다.
- 타겟이 0일 경우 첫 번째 항은 0이 되므로 두 번째 항만 계산하면 됩니다. 예측값이 0에 가까워야 손실 함수가 작습니다. 예측값이 1에 가까울수록 손실 함수는 증가합니다. 로그를 취하면 예측값이 0에서 멀어질수록 손실 함수에 일종의 페널티가 가해집니다.
이제 미분 가능하면서 자동으로 페널티까지 가해진 손실 함수가 만들어졌습니다. SGD는 이 손실 함수의 기울기를 이용해서 최적해를 찾아갑니다. 다중 분류일 경우 손실 함수는 크로스엔트로피 손실 함수를 사용합니다. 너무 이론적인 내용이 될 것 같아서 여기에는 적지 않겠습니다. 사실 몰라서 못 적는 겁니다. 대신 관련 내용을 멋지게 강의 해주신 페가님 영상을 아래에 붙입니다. 페가님 사랑해요.
설명이 길어졌으니, 이제 실습을 해보겠습니다.
6. 확률적 경사 하강법 실습
데이터를 불러오고 훈련/테스트 세트로 나눈 후 표준화 전처리까지 한방에 갑니다.
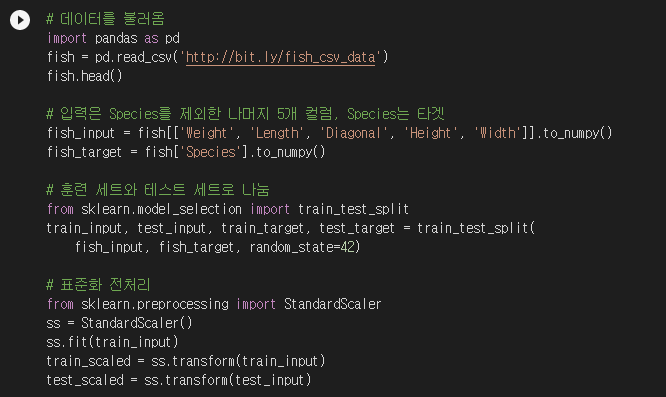
SGD 분류 알고리즘은 사이킷런의 SGDClassifier를 사용합니다. 참고로 SGD 회귀 알고리즘은 SGDRegressor입니다. 데이터를 주고 훈련까지 시켜보겠습니다.
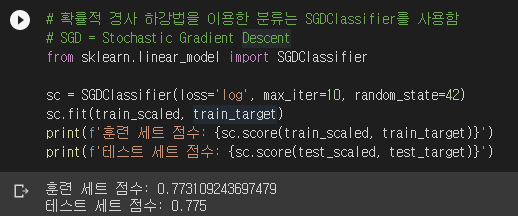
SGDClassifier의 파라미터 loss에서 손실 함수의 종류를 정할 수 있습니다. 여기에 ‘log’라고 적으면 로지스틱 회귀가 됩니다. loss의 기본값은 서포트 벡터 머신support vector machine(SVM)을 수행하는 ‘hinge’입니다. 알아둬야 할게 하나 있습니다. 코랩의 사이킷런은 v1.0.2입니다. 사이킷런 버전은 아래와 같이 알아낼 수 있습니다.
공식 문서를 보니 v1.1부터는 ‘log_loss’를 쓰라고 하네요. ‘log’는 1.3부터는 없어진다고 하니 참고하시기 바랍니다.
위 코드는 훈련 세트를 10 에포크를 실행한 겁니다. SGDClassifier 객체를 만들 때 설정한 max_iter 값이 fit()의 에포크 횟수가 됩니다. 결과를 보니 과소적합이군요. 에포크를 한번 더 실행해보겠습니다. 기존 모델을 추가 훈련시킬 때에는 partial_fit() 메서드를 사용합니다. partial_fit()은 기존에 학습한 계수와 절편을 업데이트 합니다. fit()은 이전에 학습한 계수와 절편을 모두 버리고 새로 학습합니다.
점수가 올라갔군요. 왜 테스트 세트의 점수가 교재와 다른지 의문입니다만, 일단 넘어가겠습니다. partial_fit()은 1 에포크만 실행합니다. 내부적으로 max_iter=1로 설정된다고 공식 문서에 잘 나와있네요.
참고로 SGDClassifier에 훈련 세트 전체를 넣었지만 알아서 샘플을 하나씩 꺼내서 훈련합니다. 샘플을 여러 개씩 묶어서 훈련하는 방법도 있으며 미치배치 경사 하강법minibatch gradient descent이라고 부릅니다. 아예 한번의 업데이트를 위해 세트 전체를 이용하는 방법도 있으며 배치 경사 하강법batch gradient descent이라고 부릅니다. 배치 경사 하강법은 경로가 제일 부드럽게 나오지만 메모리 사용량이 너무 많다는 단점이 있어서 잘 쓰지 않는다고 하네요. 미니배치 경사 하강법은 미니배치의 크기를 얼마로 하느냐에 따라 성능이 달라질 수 있습니다. 미니배치의 크기는 모델이 학습할 수 없고 사람이 정해주어야 하는 하이퍼파라미터입니다. 아쉽게도 SGDClassifier는 미니배치 경사 하강법이나 배치 경사 하강법은 지원하지 않습니다.
7. 에포크와 과대/과소적합
SGD에도 과대/과소적합이 일어날 수 있습니다. SGD는 기본적으로 아주 천천히 경사를 내려갑니다. 그래서 수십-수백의 에포크가 필요합니다. 에포크 횟수가 충분하지 않으면 학습이 덜 된 과소적합이 될 수 있습니다. 그런데 에포크 횟수가 너무 커도 문제가 될 수 있습니다. 훈련 세트로만 주구장창 훈련하면 훈련 세트에만 잘 맞는 과대적합이 될 수 있습니다.
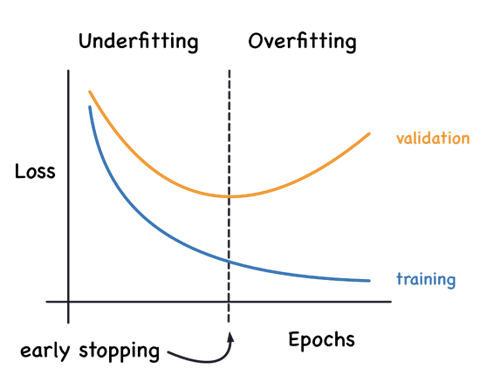
그래서 훈련/테스트 세트의 점수가 벌어지기 전에 훈련을 멈춰야 합니다. 이걸 조기 종료early stopping라고 부른다고 하네요.
훈련 세트 점수는 에포크가 진행될수록 꾸준히 증가하지만 테스트 세트 점수는 어느 순간 감소하기 시작합니다. 바로 이 지점이 모델이 과대적합되기 시작하는 곳입니다. 과대적합이 시작하기 전에 훈련을 멈추는 것을 조기 종료early stopping라고 합니다.
박해선, 혼자 공부하는 머신러닝 + 딥러닝, 한빛미디어, 210쪽
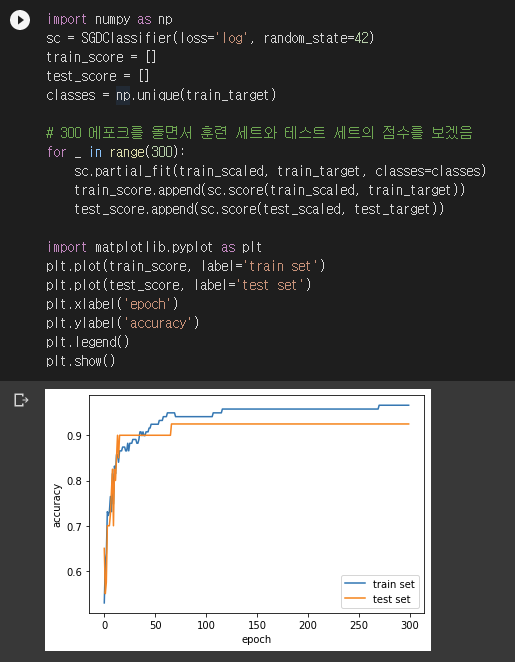
에포크를 300번 돌면서 훈련/테스트 세트의 점수를 확인해보겠습니다.
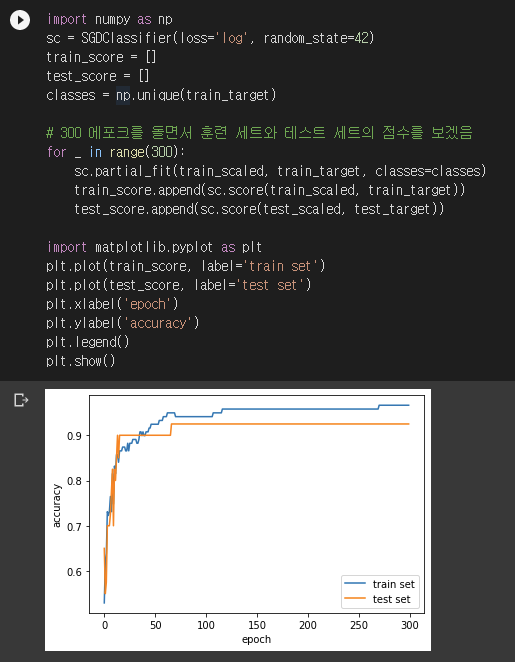
for문 바로 아래를 보면 classes 인자를 전달하고 있습니다. partial_fit()으로 추가 에포크를 돌릴 때 꼭 모든 분류 클래스가 포함된다는 보장이 없습니다. 그래서 어떤 클래스들이 포함되어 있는지 알려줘야 합니다. 결과를 보니 100 에포크를 돌렸을 때가 제일 값이 괜찮아 보이네요.
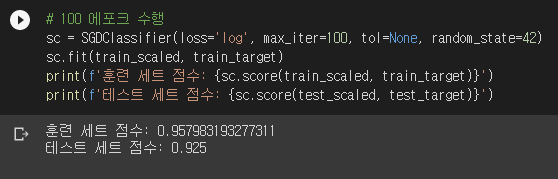
SGDClassifier의 tol은 tolerance입니다. 지정한 횟수만큼 에포크를 반복할 동안 손실 함수가 tol만큼 나아지지 않으면 훈련을 멈춥니다. 지정한 횟수는 n_iter_no_change에 들어있으며 기본값은 5입니다. tol의 기본값은 1e-3입니다. tol에 None을 넣으면 자동으로 멈추지 않고 max_iter 에포크를 무조건 반복합니다.
8. 기본 미션: 04-1 확인 문제 2번 풀이과정 설명
로지스틱 회귀가 이진 분류에서 확률을 출력하기 위해 사용하는 함수는?
1) 시그모이드 함수
2) 소프트맥스 함수
3) 로그 함수
4) 지수 함수
답은 1) 시그모이드 함수입니다. 로지스틱 회귀 결과의 z 값은 임의의 실수인데, 시그모이드 함수를 이용하면 이것을 $(0, 1)$ 범위의 확률값으로 만들 수 있습니다. 다중 분류에는 소프트맥스 함수를 사용합니다.
9. 선택 미션: 04-2 과대적합/과소적합 코랩 화면 캡쳐
4장 내용정리는 여기서 마치겠습니다. 끝까지 읽어주셔서 고맙습니다. 공부에 도움 주신 코봉님, 정도전님, 엘카인님, Ju Repi님께 감사 말씀 드립니다.
'혼공머신' 카테고리의 다른 글
| [혼공머신] 6장. 비지도 학습: 비슷한 과일끼리 모으자! (0) | 2022.08.14 |
|---|---|
| [혼공머신] 5장. 트리 알고리즘: 화이트 와인을 찾아라! (0) | 2022.07.31 |
| [혼공머신] 3장. 회귀 알고리즘: 농어의 무게를 예측하라! (0) | 2022.07.17 |
| [혼공머신] 2장. 데이터 다루기: 수상한 생선을 조심하라! (0) | 2022.07.10 |
| [혼공머신] 1장. 나의 첫 머신러닝: 이 생선의 이름은 무엇인가요? (0) | 2022.07.09 |