티스토리 뷰
(한빛미디어에서 모집하는 혼공학습단 활동의 일환으로 혼자 공부하는 머신러닝+딥러닝 책을 공부하고 작성한 글입니다. 책은 제 돈으로 샀습니다. 본문의 코드는 책의 소스코드를 기반으로 하되 글 흐름에 맞게 수정한 것입니다. 원본 코드는 저자 박해선 님의 깃허브에서 보실 수 있습니다. 책에 나오는 넘파이, 판다스 등의 내용은 본 글에는 자세히 넣지 않았습니다. 본 글의 코드는 제 깃허브에서 보실 수 있습니다.)
합성곱convolution을 이용한 딥러닝
합성곱을 간단하게 설명하기는 쉽지 않습니다. 책에서는 도장에 비유하고 있는데, 찰떡같이 와닿는 느낌은 아닙니다. 그래도 굳이 설명하자면, 두 함수의 합성곱을 계산하는 방법은 아래와 같습니다.
- 두 함수 $f(x)$와 $g(x)$의 곱을 전체 영역에서 적분합니다.
- $g(x)$를 $\tau$만큼 shift 시켜 $g(x-\tau)$로 만듭니다.
- 두 함수 $f(x)$와 $g(x-\tau)$의 곱을 전체 영역에서 적분합니다.
- $g(x-\tau)$를 $\tau$만큼 shift 시켜 $g(x-2\tau)$로 만듭니다.
- 두 함수 $f(x)$와 $g(x-2\tau)$의 곱을 전체 영역에서 적분합니다.
- 이 과정을 반복하여 $\tau$에 대한 적분값의 변화를 그래프로 그립니다.
아래는 이 과정을 gif로 만든 것입니다.

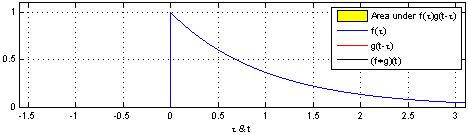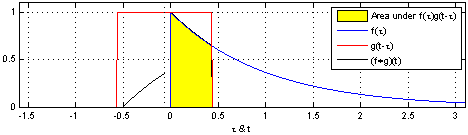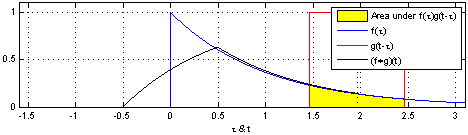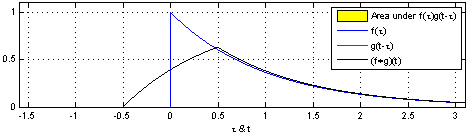
합성곱에 대해서는 여기에도 잘 설명되어 있네요. 확인해보시기 바랍니다. 좀 더 정확한 수학적 정의와 특성을 알고 싶다면아래 영상을 보시기 바랍니다. 티셔츠 시강 주의하시고요.
합성곱이 중요한 이유는, 우리가 소위 신호 필터링이라고 부르는 것이 사실 필터와 신호의 합성곱 계산이기 때문입니다. 신호의 노이즈를 줄이는 low pass filter, 엣지를 강조하는 high pass filter, 이미지를 흐릿하게 만드는 blurring, 이미지를 선명하게 만드는 sharpening 모두 합성곱 계산에 기반을 두고 있습니다. 아래는 이미지 필터링과 합성곱의 개념을 설명한 영상입니다. 다양한 필터에 대해 이미지가 어떻게 변하는지를 보여주는 좋은 영상입니다…만, 좀 깁니다. 앞부분만 보셔도 충분할 듯 하네요.
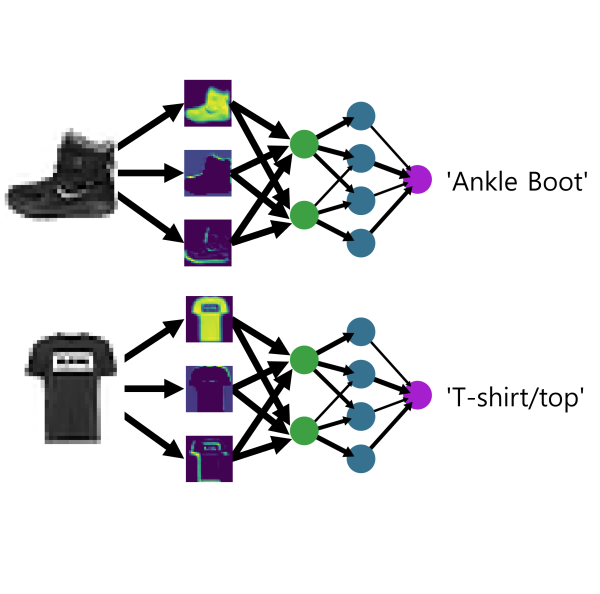
그럼 딥러닝을 하는데 왜 합성곱이 나올까요? 예를 들어보죠. 아래의 이미지들은 하나의 이미지를 다양하게 처리한 것들입니다.
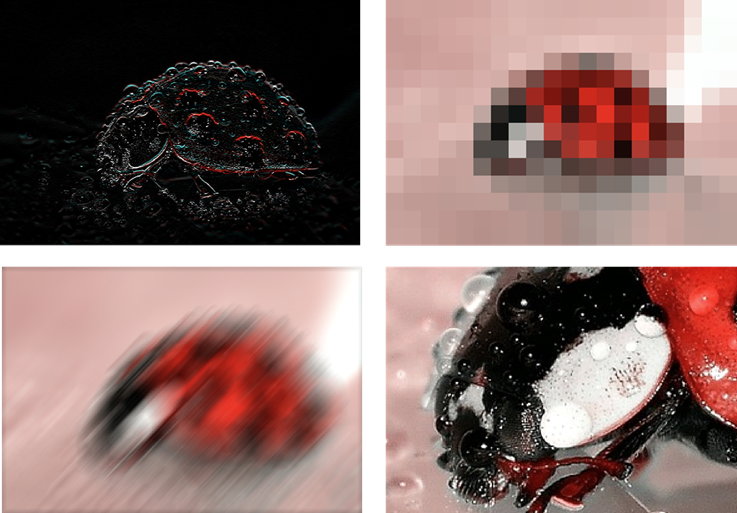
원본 이미지가 무엇이었을지 짐작이 되시나요?

귀여운 무당벌레입니다. 벌레 무서워하는 분들에겐 귀엽지 않을 수도 있겠군요. 사람은 이 이미지를 보면 무당벌레임을 바로 알 수 있습니다. 컴퓨터는 모릅니다. 컴퓨터에겐 그저 빨강 초록 파랑 신호의 조합일 뿐입니다. 그래서 딥러닝을 훈련시킬 때 원본 이미지를 그대로 사용하는 것이 아니라, 다양한 필터를 거친 이미지를 사용하는 겁니다. 위의 원본 이미지는 크기가 960 x 540입니다. 컬러 채널을 고려한다 해도 값이 150만개 밖에(?) 되지 않습니다. 여기에 필터를 10개 적용하면 컴퓨터가 훈련할 값이 10배로 늘어납니다. 물론 필터는 서로 달라야 합니다. 필터마다 이미지를 다르게 바꿀테고, 풍성해진 데이터를 딥러닝으로 학습시키는 겁니다. 그럼 필터는 어떻게 만들어야 할까요? 몰라도 됩니다. 컴퓨터가 알아서 만들어 주거든요. 뒤에서 좀 더 자세히 설명하겠습니다. 간단한 몇 가지 필터의 예제는 위키피디아에서 보실 수 있습니다. 필터는 커널kernel이라고 부르기도 합니다.
왜 굳이 복잡한 합성곱으로 이미지를 필터링 해서 쓸까요? 기본 딥러닝처럼 그냥 모든 픽셀을 한 줄로 쫙 펴고 다양하게 조작해서 학습시키면 안될까요? 이유가 있습니다. 이미지는 공간의 정보를 담고 있습니다. 예를 들어 무당벌레 이미지를 보면 피사체에 해당되는 픽셀은 가운데에 몰려 있습니다. 까만색은 까만색끼리, 빨간색은 빨간색끼리 모여 있습니다. 이처럼 픽셀 간의 공간적인 상관관계와 특징을 뽑아내기 위해서 이미지 필터링을 사용합니다. 비슷한 내용을 여기에서도 보실 수 있습니다. 67쪽부터 보시면 됩니다. 정말 좋은 자료니까 일독을 권합니다.
합성곱 신경망: Convolutional Neural Network
합성곱 신경망(CNN)의 구성이 처음에는 잘 와닿지 않을 수 있습니다만, 합성곱만 제대로 이해하면 그렇게 어렵지 않습니다. 아래는 CNN의 구성을 아주 짧게 요약한 것입니다. 이곳을 같이 보면서 읽으셔도 좋습니다.
합성곱 연산
가장 먼저 이미지에 합성곱 연산을 합니다. 합성곱 연산의 결과물을 특성 맵feature map이라고 부릅니다. 필터 크기는 3 x 3을 많이 사용합니다. 이미지를 그대로 합성곱 하면 크기가 줄어듭니다. 그래서 이미지의 가장자리에 값이 0인 픽셀을 덧붙입니다. 패딩padding 또는 제로 패딩zero padding이라고 부릅니다. 패딩을 하면 원본의 각 픽셀이 특성 맵에 기여하는 편차를 줄일 수 있다는 장점도 있습니다. 패션 MNIST 이미지 한 장의 크기는 28 x 28입니다. 패딩 후 합성곱을 하면 여전히 크기는 28 x 28입니다. 필터가 32개라면 28 x 28 x 32의 특성 맵이 만들어집니다. 필터에 들어갈 숫자 9개는 딥러닝 모델이 학습할 가중치입니다. 우리가 신경쓰지 않아도 됩니다. 여기에 절편 1개까지 포함하면 필터 하나의 파라미터는 10개입니다.
풀링pooling
풀링은 특성 맵의 크기를 줄이는 작업입니다. 특성 맵을 깍두기 모양으로 썰고, 각 깍두기마다 값을 하나씩만 뽑아냅니다. 하나의 깍두기에서 최대값만 뽑아내는 최대 풀링max pooling, 평균값을 뽑아내는 평균average pooling이 있습니다. 평균이 더 좋을 것 같지만 의외로 최대 풀링을 더 많이 사용합니다. 평균 풀링은 특성 맵의 특징적인 값을 희석시킬 수 있기 때문이라고 하네요. 풀링 크기가 (2, 2)라면 28 x 28 x 32였던 특성 맵은 14 x 14 x 32가 됩니다.
합성곱 연산을 한 번 더
합성곱을 한 번만 해야 한다는 규칙은 없습니다. 풀링으로 확 쪼그라든 특성 맵을 한 번 더 합성곱 할 수 있습니다. 단 이 경우 특성 맵의 깊이까지 고려해야 합니다. 풀링 후 특성 맵의 깊이는 1차 합성곱 필터의 개수와 같습니다. 2차 합성곱의 필터도 같은 깊이를 가져야 합니다. 크기 14 x 14 x 32인 특성 맵에 적용할 필터는 크기가 3 x 3 x 32입니다. 물론 이것도 모델 파라미터입니다. 필터 64개를 이용하고 패딩까지 한다면 2차 합성곱 이후 특성 맵의 크기는 14 x 14 x 64가 됩니다.
풀링
풀링도 한 번 더 합니다. 위에서 설명한 것과 같은 방식입니다. 풀링 후 특성 맵은 7 x 7 x 64입니다.
밀집층
28 x 28이었던 패션 MNIST 이미지가 7 x 7 x 64로 쪼그라들면서 깊어졌습니다. 각 7 x 7 이미지는 필터에 따라 원본 이미지의 어떤 특징을 담고 있을 겁니다. 이걸 한 줄로 쫙 펴고 밀집층에 입력으로 전달합니다. 밀집층에 대한 내용은 지난 주차 내용과 같습니다.
케라스를 이용한 CNN 구현
케라스로 CNN을 구현해 보겠습니다. 패션 MNIST 데이터셋을 불러오고, 훈련/검증/테스트 세트를 나누고 정규화까지 한방에 진행합니다.

앞서 설명한 대로 합성곱층-풀링층-합성곱층-풀링층 순서대로 층을 집어넣습니다.

합성곱층은 keras.layers.Conv2D 클래스를 사용합니다. 첫 번째 인자는 필터 개수입니다. padding=’same’으로 설정하면 필터 크기에 맞춰서 알아서 패딩을 해줍니다. 최대 풀링은 keras.layers.MaxPooling2D에서 가져옵니다. 여기까지 완료됐다면 이제 밀집층을 추가합니다. 밀집층은 Flatten이 필요합니다.
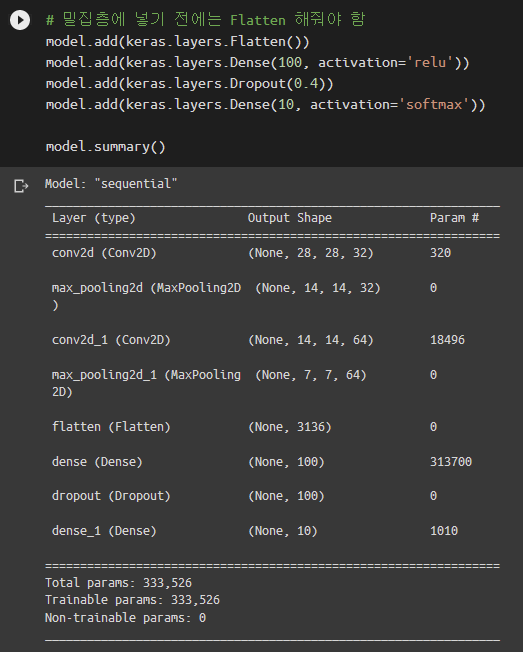
모델이 완성이 되었군요.
- 첫 번째 합성곱층의 파라미터는 320개입니다. 필터 당 파라미터가 10개이고 – 절편을 잊지 마세요 – 필터가 32개이므로 320개입니다.
- 두 번째 합성곱 층의 필터 당 파라미터 개수는 3 x 3 x 32 + 1 = 289개입니다. 289 x 64 = 18496입니다.
- 밀집층의 입력 노드 개수는 2차 풀링층의 특성 맵 픽셀 수와 같은 7 x 7 x 64 = 3136개입니다. 은닉층 노드를 100개로 만들었으므로 절편까지 고려하면 3136 x 100 + 100 = 313700입니다.
keras.utils.plot_model을 이용하면 전체 구조를 순서도처럼 볼 수 있습니다.

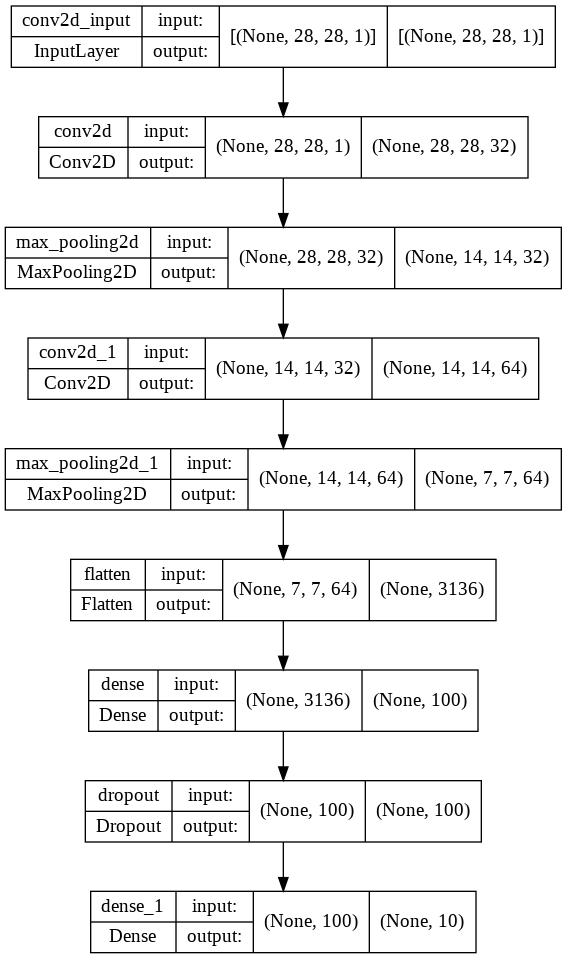
이제부터는 딥러닝이랑 똑같습니다. compile()로 옵티마이저, 손실함수를 설정하고 저장할 메트릭도 정합니다. 두 가지 콜백도 추가합니다. 체크포인트를 만들어서 에포크마다 모델을 저장하고 손실이 가장 작은 것만 남깁니다. 조기 종료를 위해 EarlyStopping도 추가합니다. 항상 그랬듯 fit()으로 훈련시키고 그 과정을 history에 저장합니다.


8 에포크의 손실이 가장 작았군요. 훈련 세트와 검증 세트의 손실함수 값을 확인해봅니다.

최적 파라미터는 이미 model에 저장되어 있습니다. 모델을 그대로 이용해서 검증 세트의 점수를 산출해봅니다.

7장에서 DNN을 이용했을 때 검증 세트 점수가 0.8848이었습니다. 0.9238로 꽤 많이 증가했습니다. 데이터셋의 이미지를 한 장 꺼내서 예측값을 보겠습니다.

가방이군요. predict()는 각 레이블에 대한 확률을 계산해줍니다. 9번째 값이 1이고 나머지는 0이군요. 여기서 주의할 점이 있습니다. predict()에 val_scaled[0]을 넣으면 안됩니다. 케라스의 fit(), evaluate(), predict()는 입력의 첫 번째 차원을 배치 차원으로 인식합니다. 즉 28 x 28 x 1 크기의 이미지 한 장을 전달하려면 1 x 28 x 28 x 1로 바꿔주어야 합니다. 28 x 28 x 1을 그대로 전달하면 28 x 1인 데이터가 28개 있는 것으로 인식합니다.
패션 MNIST의 레이블 이름은 데이터셋 안에 들어있습니다. 자세한 방법은 다른 글을 확인해주세요.

마지막으로 테스트 세트 점수도 확인해봅시다.

0.9146입니다. 훌륭하군요!
합성곱 신경망의 시각화
합성곱 신경망이 대충 어떻게 돌아가는지는 이해가 됐습니다. 여기서 좀 더 통찰력을 키우는 연습을 해보겠습니다. 실제로 필터가 어떻게 생겼는지, 필터를 거치면 원본 이미지가 어떻게 변하는지를 보겠습니다. 앞에서 모델을 hdf5 파일로 저장했습니다. 파일만 불러오면 모델을 사용할 수 있습니다.

필터는 이미지를 필터링 한다는 개념이지만 신경망의 입장에서는 가중치입니다. 가중치는 층layer의 weights에 들어있습니다. weights는 길이가 2인 리스트로, [0]에는 가중치가, [1]에는 절편이 들어있습니다.

가중치는 TensorShape이라는 자료형으로 구현되어 있습니다. 자세한 내용은 여기에 잘 설명되어 있습니다. 가중치의 분포를 한번 보겠습니다.

몇 개를 빼면 대부분 0 주위에 있군요. 각 필터가 실제로 어떻게 생겼는지 보겠습니다.


이것만 봐서는 모델이 왜 이런 필터를 만들었는지 알 수 없습니다. 7장 내용 정리에서도 말했듯이 딥러닝은 이런 부분에서 설명 가능력이 약한 것이 사실입니다. 이런 필터를 쓰면 이미지 분류가 된다는데, 왜 되는지 설명하기 어려우니까요. 대신 훈련하지 않은 필터가 어떻게 생겼는지를 보겠습니다.

아하! 가중치 값이 정규분포를 따르지 않고 균등분포가 만들어졌군요. 아마 초기값을 균등분포로 만드나 봅니다. 필터도 보겠습니다.


훈련 전에는 확실히 값들이 전부 비슷한게 보입니다. 아마 모든 필터가 비슷한 수준으로 이미지를 smoothing 하지 않을까 싶네요.
함수형 API
함수형 프로그래밍functional programming이라는 것이 있습니다. 저도 잘 모르지만, 대략의 느낌은 모든 action을 입력 - 함수 - 출력의 형태로 만들겠다는 것 같습니다. 아래는 위키피디아에서 발췌한 것입니다.
In computer science, functional programming is a programming paradigm where programs are constructed by applying and composing functions. It is a declarative programming paradigm in which function definitions are trees of expressions that map values to other values, rather than a sequence of imperative statements which update the running state of the program.
명령형imperative 프로그래밍은 결과를 “어떻게” 얻을 것인가에 중점을 두고 있다면, 선언형declarative 프로그래밍은 “무엇을” 얻을 것인가에 중점을 두고 있습니다. 그래서 선언형 프로그래밍은 겉보기에는 하나의 값에 여러 함수가 거쳐가는 것 같은 직관적인 형태를 띱니다. 다만 그런 형태를 띠기 위해 함수를 재구성해야 한다는 단점이 있습니다. 아래는 노마드 코더의 관련 영상입니다.
애초에 함수형 프로그래밍으로 설계된 클로저Clojure, 스칼라Scala, 하스켈Haskell 등의 언어도 있고, 파이썬도 함수형 프로그래밍으로 코드를 작성할 수 있습니다. 관심 있는 분들은 아래 링크들을 확인해보세요.
- 반드시 “함수형 프로그래밍”을 알아야 할까?
- 명령형(Imperative)언어와 선언형(Declarative)언어
- 함수형 프로그래밍 언어 3대장
- [ES6+: 응용] 명령형에서 함수형으로 변환시키기
- 함수형 프로그래밍이란?
케라스도 함수형 프로그래밍을 지원합니다. 함수형 API라는 녀석인데, Sequential과 add로 딥러닝 모델을 만들던 것과는 다소 방식이 다릅니다. 기존의 방식이
dense1 = keras.layers.Dense(100, activation='sigmoid')
dense2 = keras.layers.Dense(10, activation='softmax')
model = keras.Sequential()
model.add(dense1)
model.add(dense2)
이렇게 ‘층을 만든다 – 층을 더한다’의 과정이었다면, 함수형 API는
hidden = dense1(inputs)
output = dense2(hidden)
이렇게 ‘층에 입력을 넣으면 출력이 나온다’의 형태로 생겼습니다. 마치 Dense 층이 입력과 출력을 연결짓는 함수처럼 생겼달까요? 입력층은 keras.Input()으로 따로 만들어줘야 합니다.
inputs = keras.Input(shape=(784,))
그리고 마지막으로 입력과 출력을 keras.Model()에 전달하면 모델이 완성됩니다.
model = keras.Model(inputs, outputs)
앞에서 만들었던 모델을 함수형 API로 다시 만들어 보겠습니다. 우선 입력층을 keras.Input()으로 만듭니다.
input = keras.Input(shape=(28, 28, 1))
첫 번째 합성곱층과 풀링층을 만듭니다. 각 층에 입력과 출력을 적어주어야 합니다.
x = keras.layers.Conv2D(32, 3, activation='relu', padding='same')(input)
x = keras.layers.MaxPooling2D(2)(x)
두 번째 합성곱층과 풀링층도 만듭니다.
x = keras.layers.Conv2D(64, 3, activation='relu', padding='same')(x)
x = keras.layers.MaxPooling2D(2)(x)
Flatten, Dense, Dropout를 이용하여 밀집층을 구현합니다.
x = keras.layers.Flatten()(x)
x = keras.layers.Dense(100, activation='relu')(x)
x = keras.layers.Dropout(0.4)(x)
활성화 함수가 softmax인 출력층도 만듭니다.
output = keras.layers.Dense(10, activation='softmax')(x)
이제 입력과 출력을 keras.Model로 연결하기만 하면 됩니다.
model_API = keras.Model(input, output)
코드를 하나로 합치면 이렇게 생겼습니다.
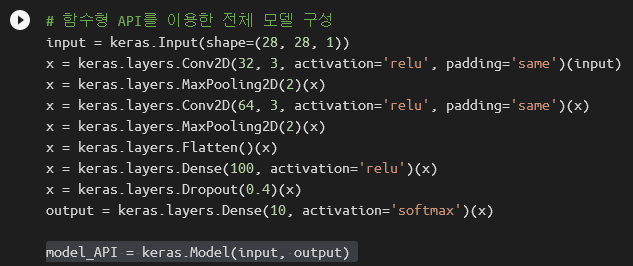
입력이 어떤 층들을 거치는지 더 잘 보이는 것 같습니다. keras.utils.plot_model()로 모델이 어떻게 생겼는지를 보니

Sequential로 만든 것과 똑같이 생겼군요. 잘 만들어진 것 같습니다.
함수형 API의 장점 1 – 모델의 중간 결과물 확인
함수형 API의 장점 두 가지를 설명하겠습니다. 첫 번째로, 딥러닝 모델의 중간 결과물을 엿볼 수 있습니다. keras.Model에 입력과 출력만 적절히 전달하면 됩니다. 예를 들어 1차 합성곱층의 결과물을 보고 싶다면, 모델 전체의 input과 1차 합성곱층의 output을 keras.Model에 입력으로 넣으면 됩니다. 모델 전체의 input은 Sequential.input에 이미 들어있습니다. 출력은 model에서 해당 층layer을 꺼낸 후 output 값을 보면 됩니다.
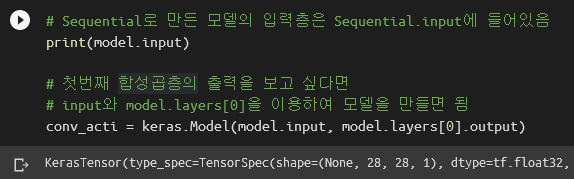
패션 MNIST의 첫 번째 샘플은

앵클부츠군요. 앞에서 만든 임시 모델 conv_acti에다가 이 샘플을 넣어보겠습니다.
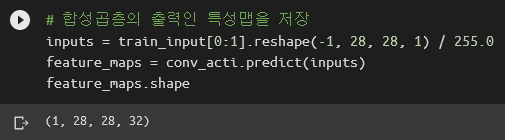
feature_maps에 1차 합성곱층이 만든 특성 맵에 들어있겠군요. 특성 맵은 필터링 된 이미지입니다. 어떻게 생겼냐면


이렇게 생겼습니다. 다양한 필터링을 통해 데이터를 풍부하게 만든다고 말씀드렸던 것이 잘 표현되어 있습니다. 어떤 이미지는 신발만 밝게, 어떤 이미지는 신발만 어둡게, 어떤 이미지는 세로 방향 경계가 밝게, 어떤 이미지는 가로 방향 경계가 밝게 표현되어 있습니다. 왜 이렇게 필터링을 했을 때 분류가 되는지는 우리는 알기 어렵습니다. 그냥 믿어야죠. 두 번째 합성곱층이 만드는 특성 맵도 보겠습니다.



음… 난해하군요. 추상화를 보는 것 같습니다. 1차 합성곱의 결과는 그래도 어느 정도 해석이 가능하기라도 했지, 2차 합성곱은 도대체 어떤 정보를 뽑고 싶었던 건지 알기 어렵습니다. 자연스러운 현상입니다. 컴퓨터는 나름대로 열심히 설명하고 있는 겁니다. 단지 사람의 뇌와는 동작방식이 너무 달라서 우리가 이해하기 어려울 뿐이죠.
함수형 API의 장점 2 – 입력 또는 출력이 여러 개인 모델 구성
함수형 API의 두 번째 장점은, 입력 또는 출력이 2개 이상인 모델을 구성할 수 있다는 점입니다. Sequential로는 불가능합니다. 케라스 홈페이지에 좋은 예시가 있어서 그대로 가져와보겠습니다. 고객의 불만사항을 접수하여 우선순위와 대응부서를 결정하고자 합니다. 딥러닝 모델로 만든다면 입출력은 아래와 같습니다.
- 입력
- 제목 (텍스트)
- 내용 (텍스트)
- 태그 (카테고리)
- 출력
- 우선순위 ($[0, 1]$ 범위의 실수)
- 대응부서 (카테고리)
코드는 아래와 같습니다. 이해가 안되어도 괜찮습니다. 사실 저도 이해 못했거든요. 전체 흐름만 이해하면 됩니다.

keras.Input()으로 입력을 3개 만들었고, title과 body에는 Embedding과 LSTM 층을 추가했으며, layers.concatenate로 모든 입력을 합친 하나의 특성 맵을 만들었습니다. 그리고 밀집층 2개는 특성 맵을 입력으로 받아서 각자의 역할을 수행하여 예측값을 내어놓습니다. 입력과 출력을 모두 keras.Model()에 전달하면 모델이 완성됩니다. keras.utils.plot_model()을 이용하면 모델이 어떻게 생겼는지 볼 수 있습니다.

8장 내용정리는 여기서 마치겠습니다. 끝까지 읽어주셔서 고맙습니다.
'혼공머신' 카테고리의 다른 글
| [혼공머신-번외편] 패션 MNIST의 레이블명을 데이터셋에서 가져오기 (0) | 2022.09.04 |
|---|---|
| [혼공머신] 혼공학습단 8기를 마무리하며 (부제: 천 줄 코딩도 import부터) (0) | 2022.08.21 |
| [혼공머신] 7장. 딥러닝을 시작합니다 (2) | 2022.08.21 |
| [혼공머신] 6장. 비지도 학습: 비슷한 과일끼리 모으자! (0) | 2022.08.14 |
| [혼공머신] 5장. 트리 알고리즘: 화이트 와인을 찾아라! (0) | 2022.07.31 |
