게으른맽랩 lazy matlab

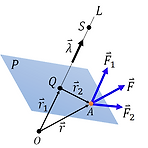
Moment of a force about an axis through the origin $O$ can be calculated in two ways: (1) $\vec{M}_{L} = \vec{r_2} \times \vec{F_2}$ (2) $\vec{M}_{L} = \vec{\lambda} \cdot \left( \vec{r} \times \vec{F} \right)$ where $\lambda$ is a unit vector in the direction of $L$, $\vec{F}_{1}$ is a component of $\vec{F}$ normal to the plane $P$, $\vec{F}_{2}$ parallel to the plane $P$, $P$ is a plane perpen..