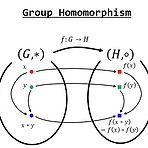
 Basic properties of group homomorphism
Basic properties of group homomorphism
Suppose f:G→G′ is a group homomorphism, and e and e′ are the identity elements of G and G′, respectively. 1. Identity preservation: f(e)=e′ pf) ∀g∈G,f(g)=f(eg)=f(e)f(g). Thus f(e)=e′. 2. Inverse preservation: ∀g∈G,f(g−1)=f(g)−1 pf) ∀g∈G,e′=f(e)=f(gg−1)=f(g)f(g−1). Thus f(g)−1=f(g−1). 3. Kern..
mathe
2025. 1. 22. 09:59
