왜 gradient가 가장 가파른 방향일까?

 

 

위 3차원 그래프를 보자. 매트랩의 peaks를 이용하면 간단히 그릴 수 있는 곡면이다.

 

점 $A$에서 움직일 수 있는 방향 중 경사가 가장 가파른 방향은 아래와 같이 주어진다.

 

$$\nabla f = \left[ \frac{\partial f(x,y)}{\partial x}, \frac{\partial f(x,y)}{\partial y} \right]^T$$

 

좋은 것에는 이름이 있다. $\nabla f$는 $f$의 gradient라고 부른다. 이름을 봐도 확실히 경사와 연관은 있어보인다. 그런데 왜 하필이면 각 방향 편미분을 성분으로 갖는 벡터가 가장 가파른 방향이 될까?

 

---

 

다루기 좋은 "이쁜" 함수라면 한 점을 계속 확대하다보면 언젠가 평면이 된다. 확대해도 평면이 되지 않는 "못생긴" 함수 또는 점은 고려하지 말자. 위 곡면을 점 $A$에서 쫙 확대해보자.

 

 

예상한 대로 평면이 되었다. 사실 약간 휘었지만 더 확대하면 분명히 거의 평면에 가까워질 것이다. 그러니 그냥 평면이라고 받아들이자. 이 평면의 등고선은 어떻게 생겼을까?

 

 

 

평면이므로 등고선은 평행한 직선들이 된다. 위에서 보면?

 

 

 

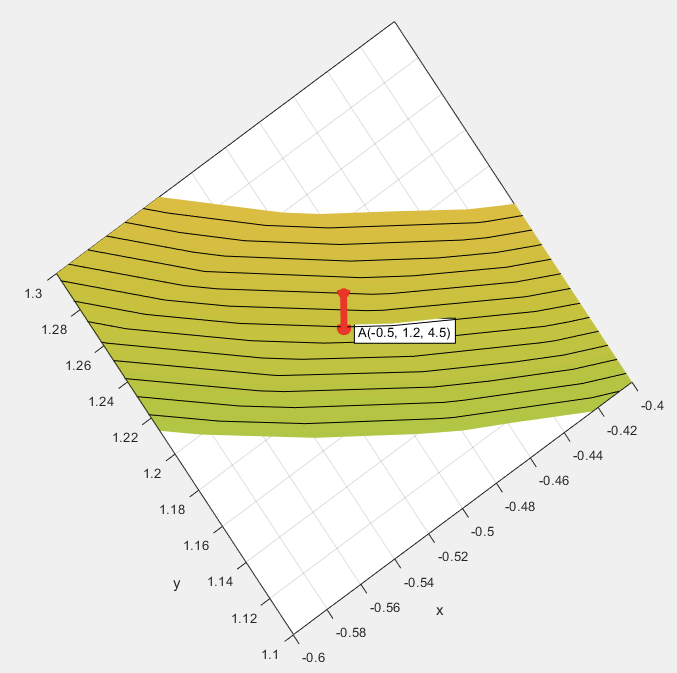
빨간 화살표는 점 $A$에서 gradient vector를 표시한 것이다. 등고선과 수직임을 알 수 있다. 평면이라면 등고선에 수직한 방향이 가장 가파른 방향일 것이다. 따라서 gradient vector가 점 $A$에서 가장 가파른 방향을 가리킴을 알 수 있다.

 

---

 

하지만 이것은 증명이 아니다. 우연히 맞았을지도 모르니까. 정말 gradient vector가 등고선에 수직인지 확인해보자. 사실 곡면을 확대하여 평면으로 만든 이유는, 평면은 모든 점에서 편미분의 값이 같으므로 다루기가 쉽기 때문이다.

 

2변수함수의 $x$ 방향 편미분이란, $y$ 값을 고정하고 $x$ 방향으로만 움직였을 때의 변화율이다. 우리는 평면을 다루고 있으므로 평면의 $x$ 방향 기울기라도 생각해도 될 것이다. 다시 말해, $x$ 방향으로 움직이는 거리에 대한 함수값 $f$의 변화의 비율을 해당 점에서의 $\partial f / \partial x$로 볼 수 있다. 마찬가지로 같은 점에서 $y$ 방향으로 움직이는 거리에 대한 함수값 $f$의 변화의 비율은 해당 점에서의 $\partial f/\partial y$로 볼 수 있다.

 

이제 한 점 $A$를 한 꼭지점으로 하는 사각형 패치를 이 평면에 놓아보자.

 

 

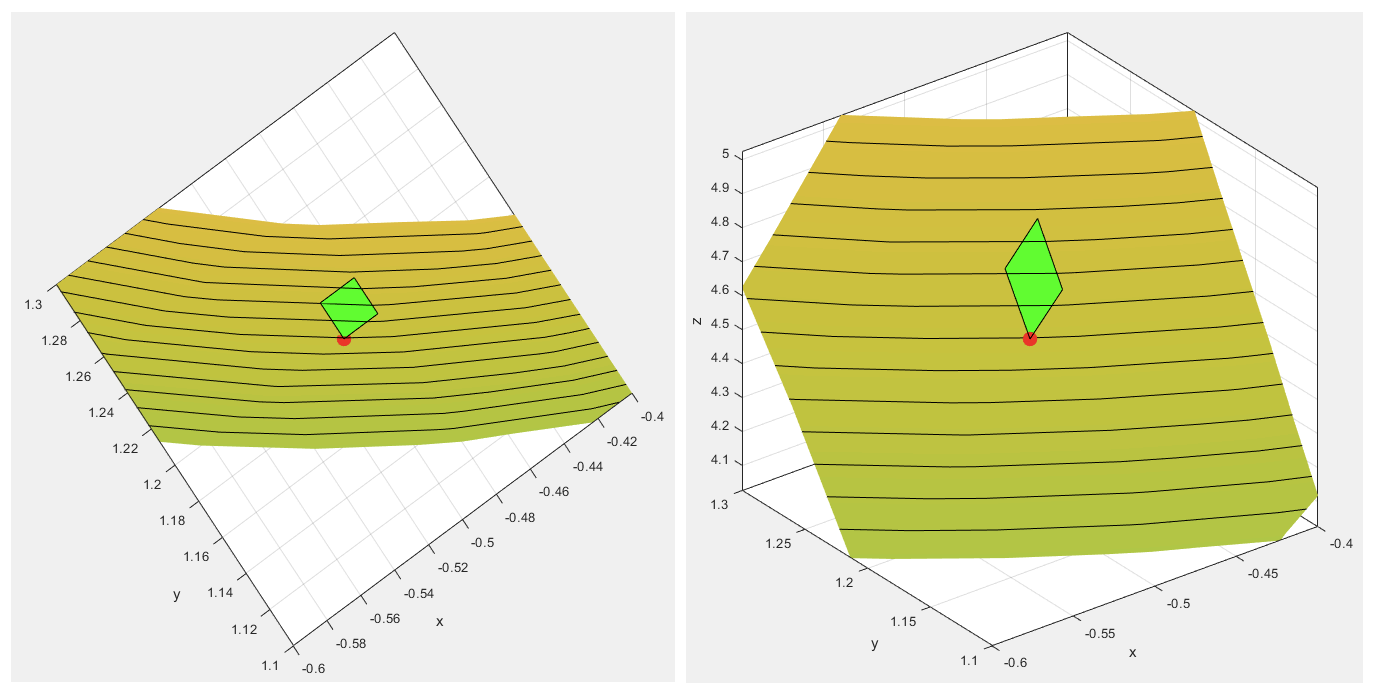
위에서 봤을 때 정사각형으로 보이는 패치이다. 실제로는 오른쪽처럼 평생하변형일 것이다. 패치의 $xy$ 평면으로의 사영인 정사각형의 한 변의 길이를 "1"이라고 하자. 별 의미는 없고 어차피 나중에 소거될 임시 값이다.

 

* 점 $A$에서 $x$축을 따라서 "1"만큼 움직이면 다른 꼭지점에 도착한다. 이때 함수값은 $\partial f/\partial x$만큼 증가한다.

* 점 $A$에서 $y$축을 따라서 "1"만큼 움직이면 다른 꼭지점에 도착한다. 이때 함수값은 $\partial f/\partial y$만큼 증가한다.

 

이걸 옆에서 보면 어떻게 생겼을까?

 

 

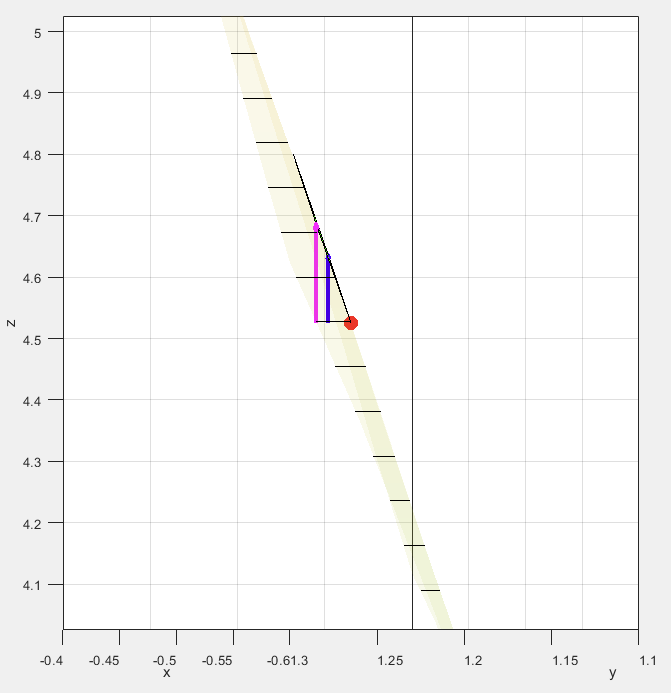
파란색 수직 화살표는 $x$축을 따라 움직였을 때 함수값 증가량이고, 자홍색 수직 화살표는 $y$축을 따라 움직였을 때 함수값 증가량이다. 여기에 화살표 두 개를 더 그려보자. 어떻게 그릴 거냐면,

 

 

 

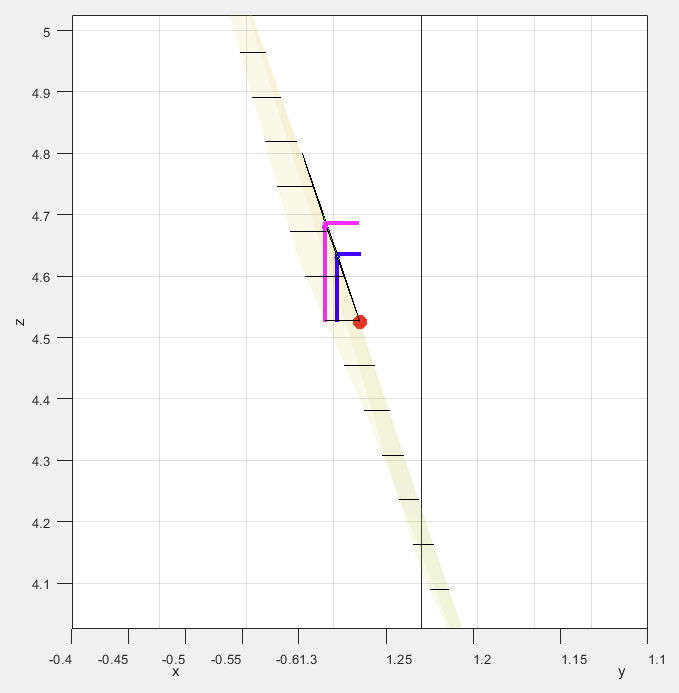
이렇게 그린다. 화살표의 정체는 아래와 같다.

 

 

 

 

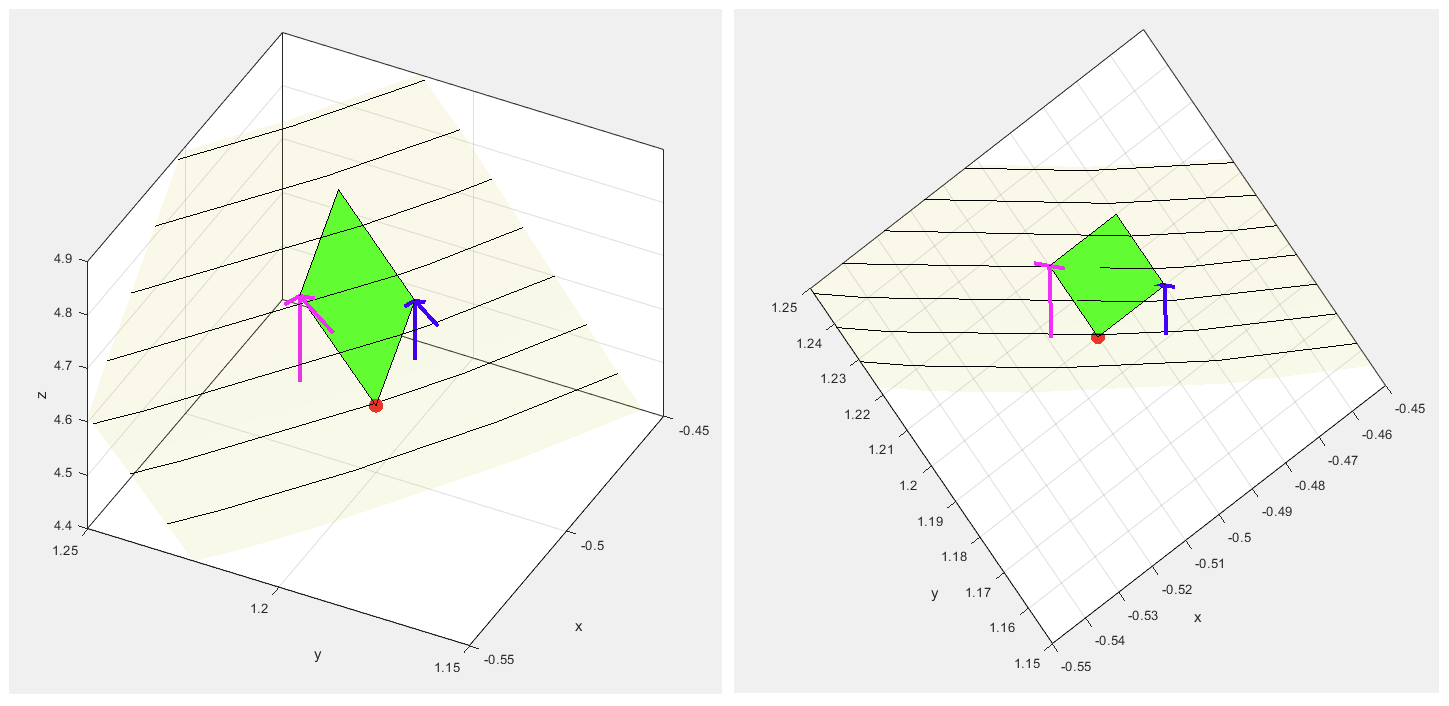
즉, 수평 화살표는 점 $A$가 포함된 등고선에서 수직으로 패치의 두 점을 향해 그린 화살표이다. 그리고 명백히 두 수직 화살표의 길이의 비율과 두 수평 화살표의 길이의 비율은 같다. 두 수직 화살표의 길이가 각각 $\partial f/\partial x$와 $\partial f/\partial y$이므로, (자홍색 수평 화살표의 길이)와 (파란색 수평 화살표의 길이)의 비율도

 

$$\frac{\partial f/\partial y}{\partial f/\partial x}$$

 

이다. 이제 거의 다 왔다. 패치를 위에서 보면 분명히 정사각형이다. 따라서파란색 화살표는 길이를 바꾸지 않도 아래처럼 이동시킬 수 있다.

 

 

 

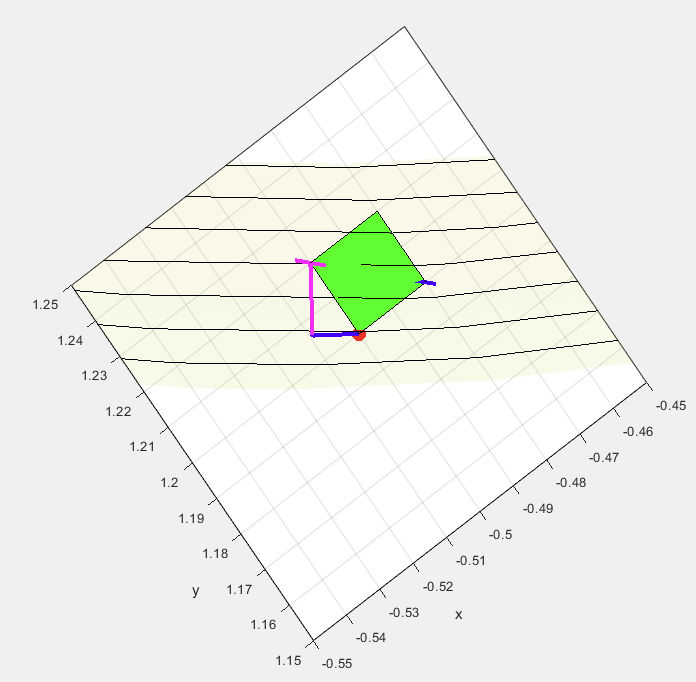
점 $A$에서 $x$ 방향으로 파란색 길이만큼 움직힌 후 $y$ 방향으로 자홍색 길이만큼 움직이면, 그 도착점은 $A$에서 봤을 때 어디에 있을까?

 

 

 

 

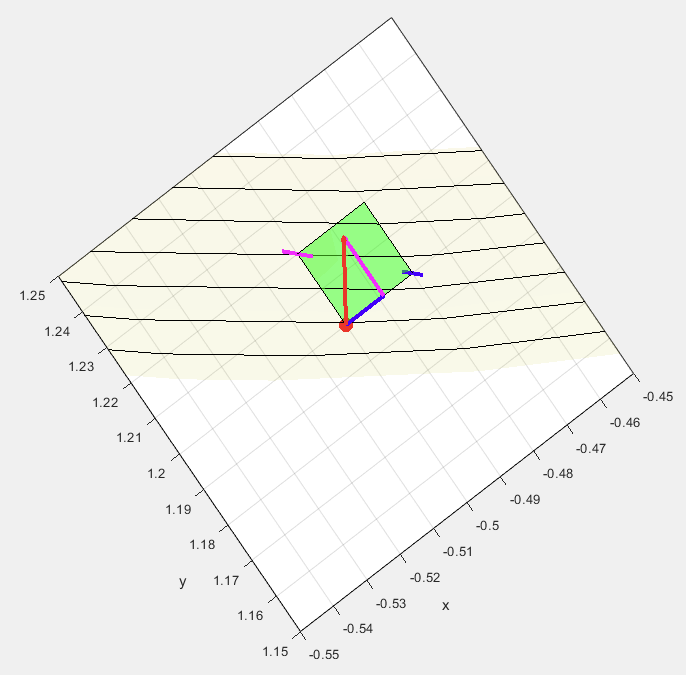
정확하게 등고선에서 수직한 방향을 가리킴을 알 수 있다. 따라서 gradient vector인

 

$$\nabla f = \left[ \frac{\partial f(x,y)}{\partial x}, \frac{\partial f(x,y)}{\partial y} \right]^T$$

 

는 등고선에 수직이므로 가장 가파른 방향이 된다.

 

아래는 위 그림들을 그린 매트랩 코드이다.

 

%% prepare peak as a symbolic function for partial diff.
syms x y f(x, y)
f(x, y) = 3*(1-x).^2.*exp(-(x.^2) - (y+1).^2) ...
    - 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2) ...
    - 1/3*exp(-(x+1).^2 - y.^2);
dfdx = diff(f, 'x');
dfdy = diff(f, 'y');

%% draw surface
[X, Y, Z] = peaks(101);
f_surf = surf(X, Y, Z);
xlabel('x'), ylabel('y'), zlabel('z')
hold on, shading interp, 
f_surf.EdgeColor = 'k';

set(gcf, 'Position', [2143 174 742 754])

%% pick a point A, draw gradient vector at A
x0 = -0.5;
y0 = 1.2;
z0 = peaks(x0, y0);

plot3(x0, y0, z0, 'ro', ...
    'MarkerFaceColor','r', ...
    'MarkerSize', 10)

txt_A = text(x0+0.2, y0-0.2, z0, sprintf('A(%.1f, %.1f, %.1f)', x0, y0, z0), ...
    'BackgroundColor', 'w', ...
    'EdgeColor', 'k');

dfdx_val = double(subs(dfdx, {'x', 'y'}, {x0, y0}));
dfdy_val = double(subs(dfdy, {'x', 'y'}, {x0, y0}));
df_val = dfdx_val^2 + dfdy_val^2;

arrow_grad3 = quiver3(x0, y0, z0, dfdx_val/30, dfdy_val/30, df_val/30, ...
    'r', 'LineWidth', 5);

% fsurf(@(x, y) z0 + dfdx_val*(x-x0) + dfdy_val*(y-y0))

keyboard

%% magnify at point A 

xlim([x0-0.1, x0+0.1])
ylim([y0-0.1, y0+0.1])
zlim([z0-0.5, z0+0.5])

arrow_grad3.AutoScaleFactor = 0.05;
txt_A.Position = [x0+0.005, y0-0.005, z0];

keyboard

%% draw countour lines

contour3(X, Y, Z, 200, 'k')
f_surf.EdgeColor = "none";

keyboard

view(-90, 90)
box on, 
ax.XAxisLocation = 'top';
view(-35, 90)

keyboard

%% place a patch on A

txt_A.Visible = 'off';
arrow_grad3.Visible = 'off';
view(-35, 90)

dx = 0.02;
dy = 0.02;

p = patch( ...
    [x0, x0+dx, x0+dx, x0], ...
    [y0, y0, y0+dy, y0+dy], ...
    [z0, peaks(x0+dx, y0), peaks(x0+dx, y0+dy), peaks(x0, y0+dy)], 'g');

keyboard

view(3)

keyboard

%% add arrows to finalize the proof

view(-123, 0)
f_surf.FaceAlpha = 0.1;
p.FaceAlpha = 0.5;

arrow_xup = quiver3(...
    x0+dx, y0, z0, ...
    0, 0, peaks(x0+dx, y0)-z0, ...
    'b', 'LineWidth', 3, ...
    'AutoScaleFactor', 1);

arrow_yup = quiver3(...
    x0, y0+dy, z0, ...
    0, 0, peaks(x0, y0+dy)-z0, ...
    'm', 'LineWidth', 3, ...
    'AutoScaleFactor', 1);

keyboard

gradvec_unit = [dfdx_val, dfdy_val, 0];
gradvec_unit = gradvec_unit/norm(gradvec_unit);

arrow_xplanar = quiver3(...
    x0+dx-gradvec_unit(1)*dx*cos(atan2(dfdy_val, dfdx_val)), ...
    y0-gradvec_unit(2)*dx*cos(atan2(dfdy_val, dfdx_val)), ...
    peaks(x0+dx, y0), ...
    gradvec_unit(1)*dx*cos(atan2(dfdy_val, dfdx_val)), ...
    gradvec_unit(2)*dx*cos(atan2(dfdy_val, dfdx_val)), ...
    0, ...
    'b', 'LineWidth', 3, ...
    'AutoScaleFactor', 1);

arrow_yplanar = quiver3(...
    x0-gradvec_unit(1)*dy*cos(atan2(dfdx_val, dfdy_val)), ...
    y0+dy-gradvec_unit(2)*dy*cos(atan2(dfdx_val, dfdy_val)), ...
    peaks(x0, y0+dy), ...
    gradvec_unit(1)*dy*cos(atan2(dfdx_val, dfdy_val)), ...
    gradvec_unit(2)*dy*cos(atan2(dfdx_val, dfdy_val)), ...
    0, ...
    'm', 'LineWidth', 3, ...
    'AutoScaleFactor', 1);

keyboard

xlim([-0.55, -0.45])
ylim([1.15 1.25])
zlim([4.4 4.9])
view(-63, 44)

keyboard

view(-36, 90)

keyboard

arrow_xup.Visible = 'off';
arrow_yup.Visible = 'off';

arrow_xplanar.XData = x0;
arrow_xplanar.YData = y0;
arrow_xplanar.ZData = z0;
arrow_xplanar.UData = -gradvec_unit(1)*dy*cos(atan2(dfdx_val, dfdy_val));
arrow_xplanar.VData = dy-gradvec_unit(2)*dy*cos(atan2(dfdx_val, dfdy_val));
arrow_xplanar.WData = 0;

keyboard

arrow_xplanar.XData = x0;
arrow_xplanar.YData = y0;
arrow_xplanar.ZData = peaks(x0+dx, y0+dy);
arrow_xplanar.UData = dx*cos(atan2(dfdy_val, dfdx_val));
arrow_xplanar.VData = 0;
arrow_xplanar.WData = 0;

keyboard

arrow_yplanar.XData = arrow_xplanar.XData + arrow_xplanar.UData;
arrow_yplanar.YData = arrow_xplanar.YData + arrow_xplanar.VData;
arrow_yplanar.ZData = arrow_xplanar.ZData + arrow_xplanar.WData;
arrow_yplanar.UData = 0;
arrow_yplanar.VData = dy*cos(atan2(dfdx_val, dfdy_val));
arrow_yplanar.WData = 0;

keyboard

arrow_grad = quiver3(...
    arrow_xplanar.XData, ...
    arrow_xplanar.YData, ...
    arrow_xplanar.ZData, ...
    arrow_xplanar.UData + arrow_yplanar.UData, ...
    arrow_xplanar.VData + arrow_yplanar.VData, ...
    arrow_xplanar.WData + arrow_yplanar.WData, ...
    'r', 'LineWidth', 3, ...
    'AutoScaleFactor', 1);