티스토리 뷰

knn_example.mlx
1.35MB

- 간단한 예제를 통해 K-최근접 이웃 알고리즘(K-Nearest Neighbor; KNN)에 대해 알아보고자 한다.
- 본 예제의 내용은 한빛미디어의 책 혼자 공부하는 머신러닝+딥러닝의 내용 일부를 매트랩으로 구현한 것이다.
- 본 예제 실행을 위해서는 Statistics and Machine Learning Toolbox가 필요하다.
1. 데이터 준비
% 빙어(smelt)의 길이와 무게
smelt_length = [9.8, 10.5, 10.6, 11.0, 11.2, 11.3, 11.8, 11.8, 12.0, 12.2, 12.4, 13.0, 14.3, 15.0];
smelt_weight = [6.7, 7.5, 7.0, 9.7, 9.8, 8.7, 10.0, 9.9, 9.8, 12.2, 13.4, 12.2, 19.7, 19.9];
% 도미(bream)의 길이와 무게
bream_length = [25.4, 26.3, 26.5, 29.0, 29.0, 29.7, 29.7, 30.0, 30.0, 30.7, 31.0, 31.0, ...
31.5, 32.0, 32.0, 32.0, 33.0, 33.0, 33.5, 33.5, 34.0, 34.0, 34.5, 35.0, ...
35.0, 35.0, 35.0, 36.0, 36.0, 37.0, 38.5, 38.5, 39.5, 41.0, 41.0];
bream_weight = [242.0, 290.0, 340.0, 363.0, 430.0, 450.0, 500.0, 390.0, 450.0, 500.0, 475.0, 500.0, ...
500.0, 340.0, 600.0, 600.0, 700.0, 700.0, 610.0, 650.0, 575.0, 685.0, 620.0, 680.0, ...
700.0, 725.0, 720.0, 714.0, 850.0, 1000.0, 920.0, 955.0, 925.0, 975.0, 950.0];
% 단위: 길이=cm, 무게=gram
% 데이터 출처
% https://gist.github.com/rickiepark/b37d04a95a42ef6757e4a99214d61697
% https://gist.github.com/rickiepark/1e89fe2a9d4ad92bc9f073163c9a37a7- 주어진 데이터는 빙어(smelt)의 길이와 무게, 도미(bream)의 길이와 무게이다.
- 이제 생선의 길이와 무게만으로 빙어인지 도미인지 알아내고자 한다.
- 먼저 그래프로 데이터가 어떻게 분포하고 있는지 확인하자.
1.1 데이터 분포 확인
figure, hold on, box on
plot(smelt_length, smelt_weight, 'ro')
plot(bream_length, bream_weight, 'bo')
xlabel('length')
ylabel('weight')
legend('smelt', 'bream', 'location', 'nw')
- 빙어(smelt)와 도미(bream)가 명확히 구분되는 것을 볼 수 있다.
- 새로운 [길이, 무게] 데이터가 들어오면 빙어인지 도미인지 어떻게 구별할까?
- 새로운 데이터가 빙어와 가까우면 빙어로, 도미와 가까우면 도미로 분류하고 싶다.
- 즉, 새로운 데이터와 기존 데이터 간의 "거리"를 이용하고 싶다.
- 새로운 데이터가 기존 데이터 중 어느 클래스와 가까운지를 이용하여 분류하는 모델을 KNN 분류 모델이라고 부른다.
- 새로운 [길이, 무게]가 들어오면, 기존 데이터와의 거리를 계산하고, 그 중 가장 가까운 데이터의 클래스를 새로운 데이터의 클래스로 추정한다. 이것이 KNN의 동작 원리이다.
2. KNN 모델 생성 및 테스트
2.1 데이터 준비
- KNN 모델은 함수 fitcknn으로 만든다.
- 우선 빙어, 도미의 길이, 무게를 fitcknn이 받을 수 있는 형태로 만들어주어야 한다.
- X에는 측정값인 길이와 무게를, Y에는 정답을 넣는다.
X = [smelt_length(:) smelt_weight(:);
bream_length(:) bream_weight(:)];
Y = [repmat("smelt", length(smelt_length), 1);
repmat("bream", length(bream_length), 1)];>> disp([X(1:5, :), Y(1:5)])
"9.8" "6.7" "smelt"
"10.5" "7.5" "smelt"
"10.6" "7" "smelt"
"11" "9.7" "smelt"
"11.2" "9.8" "smelt"
>>
>> disp([X(end-4:end, :), Y(end-4:end)])
"38.5" "920" "bream"
"38.5" "955" "bream"
"39.5" "925" "bream"
"41" "975" "bream"
"41" "950" "bream"
>>
2.2 모델 생성
- 이제 KNN 모델을 만들자.
>> Mdl = fitcknn(X, Y)
Mdl =
ClassificationKNN
ResponseName: 'Y'
CategoricalPredictors: []
ClassNames: {'bream' 'smelt'}
ScoreTransform: 'none'
NumObservations: 49
Distance: 'euclidean'
NumNeighbors: 1
Properties, Methods
>>- fitcknn은 ClassificationKNN 객체를 반환한다.
- 이 객체는 KNN 모델을 관리하는 매니저이다.
- 매니저는 필요한 모든 정보(Properties)를 갖고 있으며 여러 가지 일(Methods)을 시킬 수 있다. (
마치 대학원생처럼) - ClassNames를 보니 분류할 Class가 알아서 들어갔다.
- NumObservations에는 내가 넣은 데이터 개수가 들어갔다.
- Distance가 euclidean이라고 한다. 거리를 재는 방법을 말한다. 피타고라스 정리를 생각하면 된다. 참고로 거리를 재는 방법은 여러 가지가 있다.
- NumNeighbors도 중요한데 이건 좀 이따가 알아보자.
2.3 모델 테스트
- 길이 30cm, 무게 600g인 생선은 빙어일까, 도미일까?
new_length = 30;
new_weight = 600;
figure, hold on, box on
plot(smelt_length, smelt_weight, 'ro')
plot(bream_length, bream_weight, 'bo')
plot(new_length, new_weight, 'go', 'MarkerFaceColor', 'g')
xlabel('length')
ylabel('weight')
legend('smelt', 'bream', 'unknown', 'location', 'nw')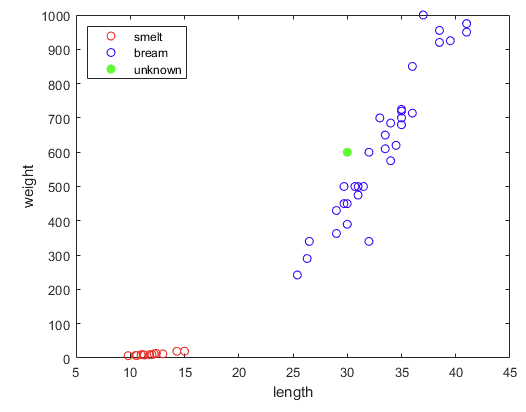
- 파란 점들에 가까이 있으므로 도미여야 할 것 같다. 모델한테 물어보자.
>> Mdl.predict([new_length, new_weight])
ans =
1×1 cell array
{'bream'}- 오, 맞췄다!
- 길이 12cm, 무게 10g인 생선은 빙어겠지?
>> new2_length = 12;
>> new2_weight = 10;
>> Mdl.predict([new2_length, new2_weight])
ans =
1×1 cell array
{'smelt'}
>>- 잘하잖아?
3. 스케일링
3.1 스케일을 맞춰야 하는 이유
- 길이가 25cm, 무게가 110g인 생선은 빙어일까, 도미일까?
new3_length = 25;
new3_weight = 110;
figure, hold on, box on
plot(smelt_length, smelt_weight, 'ro')
plot(bream_length, bream_weight, 'bo')
plot(new3_length, new3_weight, 'go', 'MarkerFaceColor', 'g')
xlabel('length')
ylabel('weight')
legend('smelt', 'bream', 'unknown', 'location', 'nw')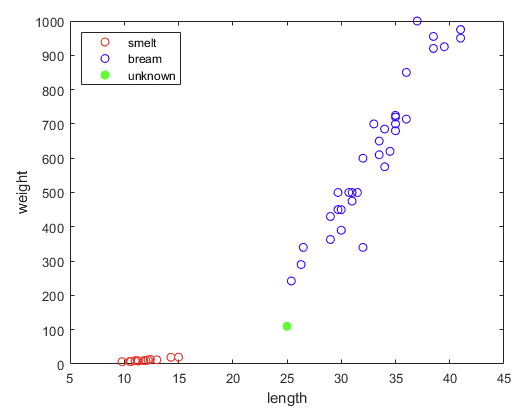
- 딱 봐도 도미잖아?
>> Mdl.predict([new3_length, new3_weight])
ans =
1×1 cell array
{'smelt'}- 안되잖아?

- 문제는 스케일이다. 그래프를 보면 길이보다 무게의 스케일이 훨씬 큰 것을 알 수 있다.
- 어차피 컴퓨터가 보는 것은 숫자 뿐이다. 숫자를 같은 스케일로 맞추면 어떻게 보일까?
figure, hold on, box on, axis equal
plot(smelt_length, smelt_weight, 'ro')
plot(bream_length, bream_weight, 'bo')
plot(new3_length, new3_weight, 'go', 'MarkerFaceColor', 'g')
xlabel('length')
ylabel('weight')
legend('smelt', 'bream', 'unknown', 'location', 'nw')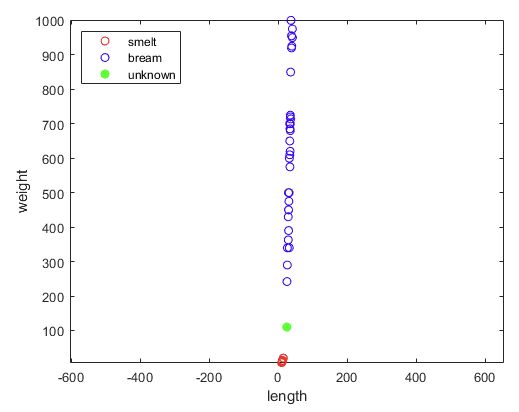
- 왜 새로운 생선을 빙어로 추정했는지 알 것 같다.
- 스케일을 맞췄더니 데이터가 그냥 한 줄이다.
- KNN은 데이터 간의 거리를 이용하는데, 이래서는 생선의 길이는 별 의미가 없다.
- 사실상 무게만으로 분류를 하고 있었던 것이다.
- 위에서 봤던 그래프는 길이가 뻥튀기 되어 있었던 것이다! (
과대포장이 이렇게 위험하다.)
3.2 최근접 이웃 데이터 찾기
- 실제로 새로 들어온 데이터와 가장 가까운 기존 데이터가 무엇인지 직접 볼 수도 있다.
- knnsearch 함수를 이용하면 된다.
>> [idx, D] = knnsearch(X, [new3_length, new3_weight])
idx =
14
D =
90.653
>> [X(idx,:) Y(idx)]
ans =
1×3 string array
"15" "19.9" "smelt"
>>- 하필이면 가장 큰 빙어에 걸렸다.
- 새로운 생선의 무게 110과 가장 큰 빙어의 무게 19.9의 차이는 90.1이다.
- knnsearch는 신규 데이터와 가장 가까운 기존 데이터와의 거리도 반환해준다.
- 반환값이 90.653이다. 90.1과 거의 차이가 없다.
- 사실상 무게만으로 분류하고 있었다는 증거이다.
3.3 스케일 맞춰주기
- 길이와 무게를 비슷한 중요도로 다루기 위해 두 값의 스케일을 비슷하게 맞춰주어야 한다.
- 가장 자연스러운 방법은, 생선의 길이와 무게가 모두 정규분포를 따른다고 가정하고 평균을 0, 표준편차를 1로 맞추는 방법이다.
- 표준점수standard score라고도 부르고 z점수z score라고도 부르는 방법이다.
X_mean = mean(X);
X_std = std(X);
X_scaled = (X - X_mean)./X_std;- 스케일을 맞춘 후 다시 그래프를 그려보자.
- 새로운 생선 데이터도 같은 방법으로 스케일을 맞춰주어야 함에 주의하자.
new3_length_scaled = (new3_length - X_mean(1))/X_std(1);
new3_weight_scaled = (new3_weight - X_mean(2))/X_std(2);
figure, hold on, box on, axis equal
plot(X_scaled(1:14,1), X_scaled(1:14,2), 'ro')
plot(X_scaled(15:end,1), X_scaled(15:end,2), 'bo')
plot(new3_length_scaled, new3_weight_scaled, 'go', 'MarkerFaceColor', 'g')
xlabel('length (scaled)')
ylabel('weight (scaled)')
legend('smelt', 'bream', 'unknown', 'location', 'nw')
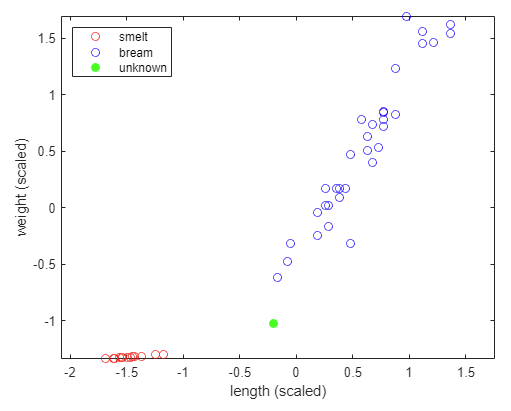
- 길이와 무게가 비슷한 스케일로 맞춰진 것을 볼 수 있다.
- 새로운 생선의 클래스를 다시 확인해보자.
- 데이터의 스케일을 바꿨으므로 모델도 다시 만들어야 한다.
>> Mdl = fitcknn(X_scaled, Y);
>> Mdl.predict([new3_length_scaled, new3_weight_scaled])
ans =
1×1 cell array
{'bream'}
>>- 원하던 대로 도미로 분류했음을 알 수 있다.
4. 최근접 최대 몇개? (aka 최최몇)
- 숫자만 봐도 명백한 경우는 사실 재미가 없다.
- 길이가 10cm 근처이고 무게가 10g 근처이면 굳이 모델 안 돌려봐도 빙어겠지.
- 중요한 것은 애매한 데이터를 어떻게 처리하느냐이다.
- 일부러 애매한 데이터를 만들어보자.
new4_length = 21;
new4_weight = 110;
new4_length_scaled = (new4_length - X_mean(1))/X_std(1);
new4_weight_scaled = (new4_weight - X_mean(2))/X_std(2);
figure, hold on, box on, axis equal
plot(X_scaled(1:14,1), X_scaled(1:14,2), 'ro')
plot(X_scaled(15:end,1), X_scaled(15:end,2), 'bo')
plot(new4_length_scaled, new4_weight_scaled, 'go', 'MarkerFaceColor', 'g')
xlabel('length (scaled)')
ylabel('weight (scaled)')
legend('smelt', 'bream', 'unknown', 'location', 'nw')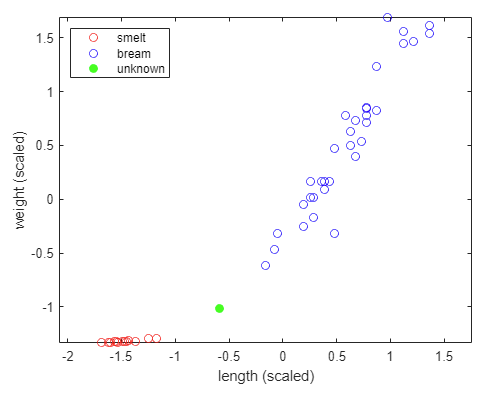
- 요거요거 애매하다.
- 모르겠으니까 가장 가까운 데이터가 무엇인지 찾아보자.
- 어쨌든 우리는 최근접 이웃(Nearest Neighbor) 알고리즘을 배우는 중이니까.
>> idx = knnsearch(X_scaled, [new4_length_scaled, new4_weight_scaled])
idx =
15
>> [X(idx,:), Y(idx)]
ans =
1×3 string array
"25.4" "242" "bream"
>>- 전체 데이터 중 앞 14개가 빙어, 그 뒤가 도미였다.
- 15번, 즉 가장 작은 도미가 최근접 데이터이므로 새로운 생선도 도미여야 할 것 같다.
- 그런데 말입니다.
- 가장 가까운 데이터 5개를 보면 어떨까?
>> knnsearch(X_scaled, [new4_length_scaled, new4_weight_scaled], 'K', 5)
ans =
15 14 13 16 12
>>- 오우 지쟈스.
- 가장 가까운 5개 중 3개가 빙어이다.
- 이럴 땐 빙어라고 해야 할까, 도미라고 해야 할까?
- 정답: 맘대로 하면 된다.
- 아 모르겠고 난 최근접 데이터 하나만 볼래! 라고 하면 하나만 보면 된다.
- 에이 그래도 5개 정도는 봐야지...라고 하면 5개 보면 된다.
- 모델은 결과예측만 잘 하면 장땡이니까.
- 최근접 데이터 몇 개를 볼 지 정하는 것이 ClassificationKNN 객체의 NumNeighbors 속성이다. 기본값은 1이다.
>> Mdl.NumNeighbors
ans =
1
>> Mdl.predict([new4_length_scaled, new4_weight_scaled])
ans =
1×1 cell array
{'bream'}
>> Mdl.NumNeighbors = 5;
Mdl.predict([new4_length_scaled, new4_weight_scaled])
ans =
1×1 cell array
{'smelt'}
>>- NumNeighbors=1일 때에는 최근접 데이터가 도미이므로 도미로 예측했다.
- NumNeighbors=5일 때에는 최근접 5개 데이터 중 빙어가 더 많았으므로 빙어로 예측했다.
5. 마치며
- 머신러닝 기법 중 가장 간단하다고도 볼 수 있는 K-최근접 이웃 알고리즘(KNN)에 대해 알아보았다.
- KNN은 사실상 무언가를 학습하지는 않는다고도 볼 수 있다.
- 데이터 간의 거리를 계산할 뿐 업데이트 되는 것이 없기 때문이다.
- 다음에는 K-NN에 훈련 세트/테스트 세트의 개념과 샘플링 편향에 대해 알아보자.
- 게으른
'matlab' 카테고리의 다른 글
| 게으른쌤의 매트랩 책을 쓰고 있습니다. (0) | 2023.10.30 |
|---|---|
| 홍길동 기자가 쓴 기사만 찾기 (0) | 2023.10.10 |
| fprintf에 세미콜론이 없어도 되는 이유 (0) | 2023.09.05 |
| 함수 핸들 이해하기 (0) | 2023.08.31 |
| n차원 구의 부피는? (0) | 2023.08.07 |
