자연수의 개수와 짝수의 개수가 같다고?

자연수의 개수와 짝수의 개수가 같다는 게 무슨 말일까? 명백히 짝수는 자연수의 진부분집합이다. 그렇다면 자연수가 짝수보다 많다고 하는 것이 타당하지 않을까? 하지만 이게 생각만큼 간단한 문제가 아니다.
아래 집합을 보자. 여기, 외로운 과일 네 개가 있습니다.

과일 네 종류를 원소로 갖는 집합이다. 집합의 크기는 4이다. 이 집합을 아래와 같이 바꿨다.

사과 2개는 원소가 2개가 된 것이 아니고, 그냥 사과 2개를 하나로 묶은 것이다. 따라서 위와 같이 바꾼다고 해서 집합의 크기가 바뀌지는 않을 것이다. 원소가 몇 개이든 이 사실은 변함이 없다.
이번엔 아래를 보자.


집합의 크기는 달라지지 않을 것이다. 여기서 교묘하게 무한집합으로 바꾼다고 해도

두 집합의 “크기”가 달라지지는 않을 것 같다. 모든 원소에 2를 곱한다고 원소의 개수가 갑자기 많아지거나 적어지면 이상하잖은가?
이제 아래를 보자. 짝수의 집합을 원소나열법으로 적은 것이다.

당신이 잠깐 한눈을 판 사이에, 집합이 이렇게 바뀌었다.

퀴즈: 짝수 집합의 모든 원소를 2로 나눴을까? 아니면 짝수 집합을 치우고 자연수 집합을 가져온 걸까?
정답: 알 수 없다!
모든 짝수를 2로 나눈 결과는 분명히 자연수 집합과 똑같다. 자연수보다 더 많지도, 더 적지도 않은, 정확히 같은 집합이다. 또 잠깐 한눈을 판 사이에, 집합이 이렇게 바뀌었다.

원래의 짝수 집합으로 되돌려놓은 것일까? 자연수 집합의 각 원소에 2를 곱한 것일까? 역시 알 수 없다. 마찬가지로 아래의 집합도

자연수 집합의 각 원소에 4를 곱한 것인지, 짝수 집합의 각 원소에 2를 곱한 것인지, 애초에 4의 배수만 모아놓은 집합인지 알 수 없다. 아니, 정확히는 알 필요가 없다. 어떻게 만들어졌든 차이가 없는 완벽히 같은 집합이기 때문이다.
같은 집합은 크기가 같다. 이 말은 원소가 유한하든 무한하든 성립해야 할 것이다. 집합의 크기는 보통 절대값 기호를 사용한다. 즉, 이 말을 하고 싶다.

사실 생각해보면 4 대신 어떤 수가 들어가든 성립함을 알 수 있다.
여기서 한 가지 궁금증이 생긴다. 원소가 유한개이면 개수를 셀 수 있으므로 크기를 말할 수 있다. 앞에서 보았던
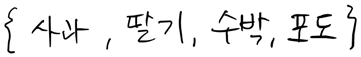
이 집합의 크기는 4이고,
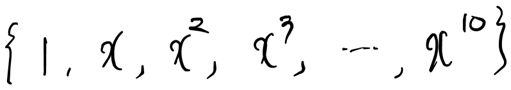
이 집합의 크기는 11이다. 하지만 자연수는? 원소가 무한개인데 크기를 얼마라고 해야 할까? 수학에서는 이것을 기수(cardinality, cardinal number)라고 부르고 자연수의 기수를 알레프-0라고 말하는데, 용어가 어려우니까 그냥 아는 기호만 써서 |자연수|라고 부르자. 기호가 뭐가 중요하겠는가? 의미가 중요하지.
|자연수|는 자연수 집합의 “크기”이자 자연수의 “개수”이다. 유한집합이라면 원소의 개수가 같은 두 집합은 자명하게 크기가 같다고 말할 수 있다. 이것을 무한집합에도 똑같이 적용하고 싶다. |자연수|=|짝수|는 무슨 의미일까? 이것 역시 유한집합의 개념을 차용하자. 아래의 두 집합은 크기가 같은가?
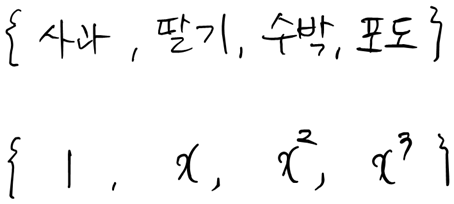
같다고 말해야 할 것 같다. 원소의 개수가 같기 때문이다. 원소의 개수가 같은지를 어떻게 아는가? 하나씩 짝지어보면 된다.
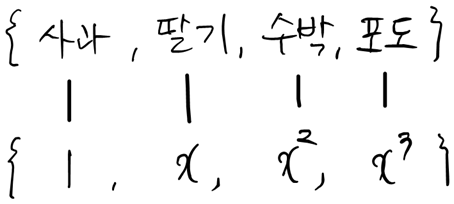
하나씩 이어서 남는 것이 없으므로, 두 집합은 크기가 같다. 짝지어서 어느 쪽에도 남는 것이 없을 때 우리는 “일대일 대응이 존재한다”라고 말한다. 즉, 두 유한집합 간에 일대일 대응이 존재하면 우리는 두 집합의 크기가 같다고 말한다. 이것을 무한집합에도 그대로 적용해보고 싶다.
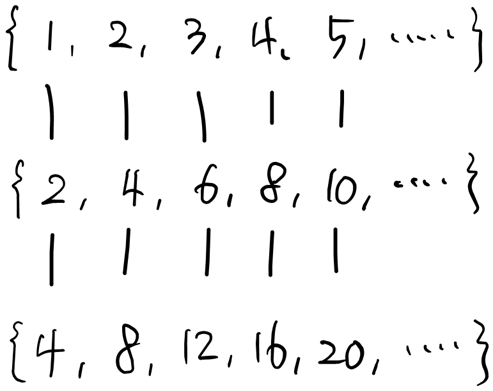
분명히 3개의 집합 간에는 일대일 대응이 존재한다. 그 어디에도 남는 것도, 부족한 것도 없다. 앞에서 보았듯이, 짝수를 모두 2로 나눈다고 집합의 크기는 바뀌지 않고, 짝수를 모두 2로 나누면 자연수 집합과 완벽히 동일해지기 때문이다. 여기서 중요한 결론에 도달한다.
두 집합 간에 일대일 대응이 존재하면 두 집합은 크기가 같다.
이 명제는 집합의 원소가 유한개이든 무한개이든 성립한다.
이제 맨 처음에 봤던 그림을 다시 보자. 낯설게 보일 것이다.
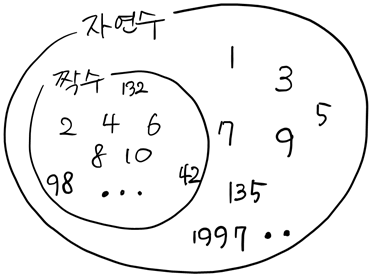
분명히 짝수는 자연수의 진부분집합이다. 자연수에서 짝수를 제거해도 여전히 무한히 많은 원소가 남기 때문이다. 하지만 자연수와 짝수 간에는 분명히 일대일 대응이 존재한다. (물론 자연수-홀수, 짝수-홀수 간에도 존재한다.) 따라서 어느 쪽이 더 많다고 말할 수 없다. 그래서 아래와 같은 기묘한 등식이 성립한다.
|자연수| + |자연수| = |자연수|
이제 무한집합이 굉장히 생소하게 느껴질 것이다. 수학에서는 무한집합을 아래와 같이 정의한다.
자신의 어떤 진부분집합과 일대일 대응이 존재하는 집합
서두에 던졌던 질문을 다시 보자. 자연수가 짝수보다 많다고 하는 것이 타당하지 않을까? 왜 이게 생각만큼 간단한 문제가 아니라는 걸까? 한편으로는 여전히 불편하다. 자신의 진부분집합과 원소의 개수가 같다니? 이렇게 주장하고 싶을 수도 있다.
나는 그래도 자연수가 짝수보다 많다고 말할래. 짝수가 자연수의 진부분집합이잖아.
이 경우 무슨 문제가 생길까? 아래 그림을 보자.
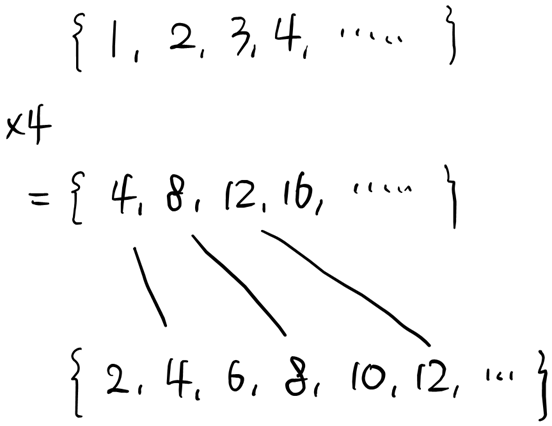
모든 자연수에 4를 곱하면 4의 배수의 집합이 된다. 원소를 더하거나 빼지 않았으므로 4의 배수는 여전히 자연수만큼 많다. 그런데 이 집합은 짝수 집합의 진부분집합이다. 만약
진부분집합은 원래 집합보다 작다.
라고 주장해버리면, 자연수는 짝수보다 많으면서 동시에 짝수보다 적다는 결론에 도달한다. 이것은 모순이다. 이 모순을 해결할 방법은
1. 무한집합은 자신의 진부분집합과 크기가 같을 수 있다고 인정하거나
2. 무한집합의 크기 개념을 포기해야 한다.
아무래도 1번이 더 좋은 방법일 것이다.
일대일 대응이 존재하는 두 집합은 크기가 같다는 논리를 이용하면 아래의 사실도 확인할 수 있다. 자연수와 일대일 대응이 되도록 나열만 할 수 있으면 된다.
|자연수| = |정수| = |유리수|
같은 논리를 실수에도 적용할 수 있다. 실수와 (0, 1)은 크기가 같다. 그 이유는 아래 그림을 보면 말이 필요없을 정도로 자명하다.
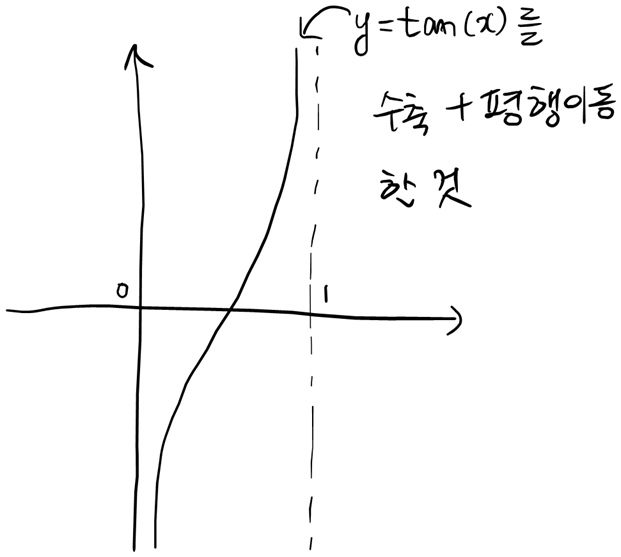
이제 자연수와 실수 중 어느 것이 더 많냐는 질문이 남는다. 이 질문은 아래 영상으로 대신한다.
딴지1. 자연수와 짝수는 수직선 상에서 밀도가 다르잖아요?
대답1. 밀도가 달라서 개수도 다른 것은 유한개일 때에만 성립한다. 무한에서는 성립하지 않을 수도 있다. 힐베르트의 무한 호텔을 생각해보자.
딴지2. 에이 그래도 유리수랑 자연수랑 개수가 같다는 건 좀 에바 아님?
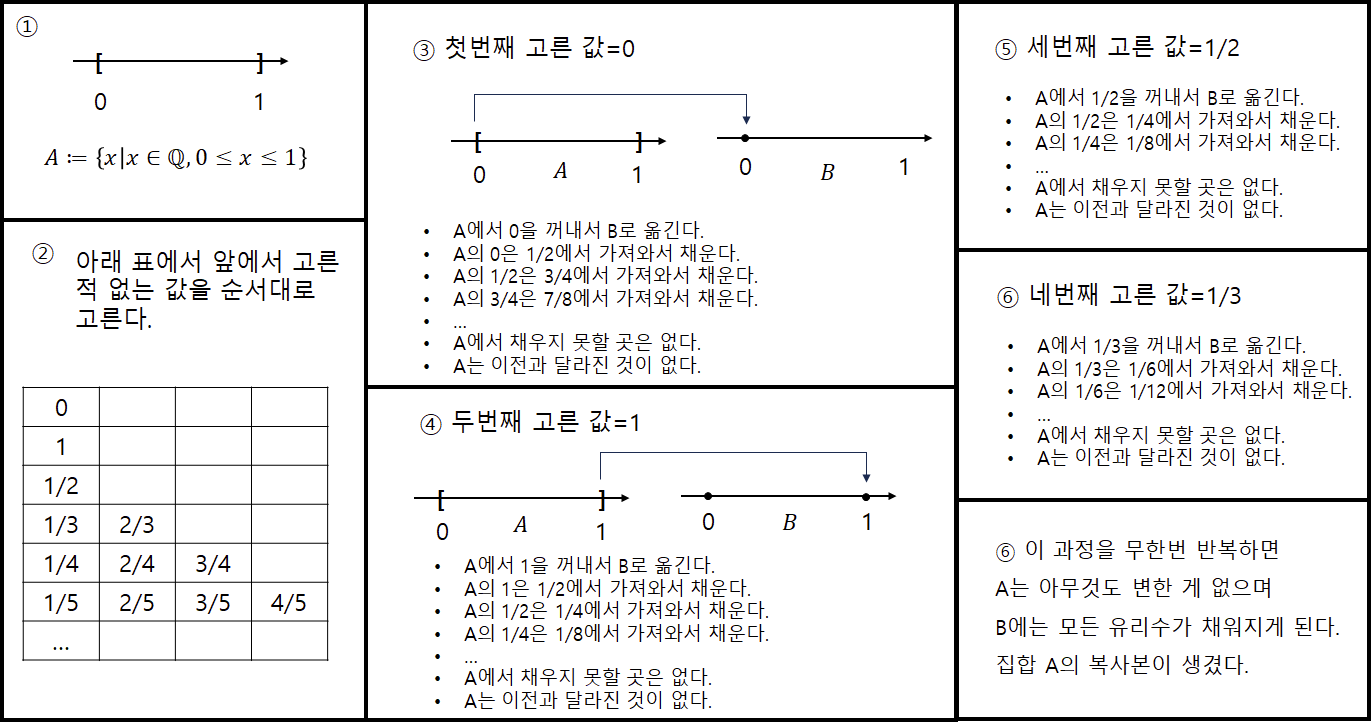
대답2. 무한을 다루다 보면 직관에 반하는 내용이 많이 나온다. 아래는 [0, 1] 범위의 유리수를 복제하는 방법이다. 논리적 모순은 없다. 이 과정으로 유리수를 얼마든지 복제할 수 있다. 따지자면 바나흐-타르스키 역설의 유리수 버전이라고 볼 수도 있겠다. |유리수|=|자연수|가 더 이상한가, 유리수의 복제가 더 이상한가?
끗
