Basic properties of group homomorphism
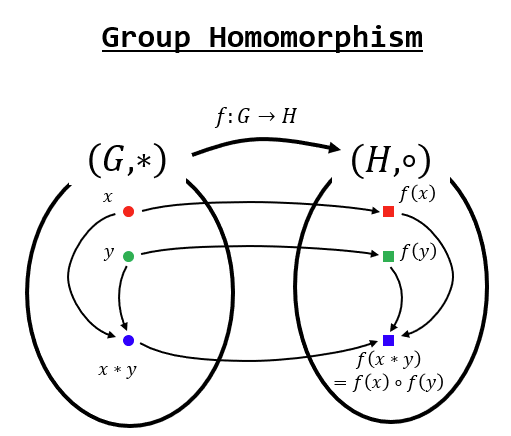
Suppose $f: G \to G'$ is a group homomorphism, and $e$ and $e'$ are the identity elements of $G$ and $G'$, respectively.
1. Identity preservation: $f(e) = e'$
pf) $\forall g\in G, f(g) = f(e\,g) = f(e) f(g)$. Thus $f(e) = e'$.
2. Inverse preservation: $\forall g\in G, f(g^{-1}) = f(g)^{-1}$
pf) $\forall g\in G, e' = f(e) = f(g\,g^{-1}) = f(g) f(g^{-1})$. Thus $f(g)^{-1} = f(g^{-1})$.
3. Kernel is a normal subgroup: $\ker f \trianglelefteq G$
pf) $\forall h\in \ker f, \forall g\in G$,
\begin{align}
f(g\,h\,g^{-1}) &= f(g) f(h) f(g^{-1}) \\
&= f(g) f(g^{-1}) = e'
\end{align}
Thus $ghg^{-1} \in \ker f$.
4. Image is a subgroup of G'.
pf) (closedness) $\forall u, v \in f(G)$, let $f(x) = u, f(y) = v$. Then
\begin{align}
uv &= f(x) f(y) \\
&= f(xy) \in f(G).
\end{align}
(identity element) $e' \in f(G)$ since $f(e) = e'$.
(inverse element) Pick any $u\in f(G)$. Let $f(x) = u$. Then
$$e' = f(e) = f(x\,x^{-1}) = f(x) f(x^{-1}) = u \, f(x^{-1})$$.
Thus $f(x^{-1})$ is the inverse of $u$.
5. 1st isomorphism thm: $G\big/ \ker f \cong f(G)$
pf) Define a function
\begin{align}
f: G\big/ \ker f &\to f(G) \\
g \ker f &\mapsto f(g)
\end{align}
(well-definedness) If $g_1 \ker f = g_2 \ker f$ for $g_1, g_2 \in G$, then
\begin{align}
g_1^{-1} g_2 &\in \ker f \\
f(g_1^{-1} g_2) &= e' \\
f(g_1^{-1})f(g_2) &= e' \\
f(g_1) &= f(g_2)
\end{align}
(1-1) If $f(g_1) = f(g_2)$, then
\begin{align}
f(g_1) &= f(g_2) \\
f(g_1^{-1} g_2) &= e' \\
g_1^{-1} g_2 &\in \ker f \\
g_1 \ker f &= g_2 \ker f
\end{align}
(onto) $\forall f(g)\in G', \exists g \ker f \in G\big/ \ker f$.
6. Image of a subgroup is a subgroup.
pf) Let $H$ be a subgrup of $G$.
(closedness) Pick any $f(x)$ and $f(y)$ from $f(G)$. Then $xy \in G$ and $f(x)f(y) = f(xy) \in f(G)$.
(identity element) Because $H \le G$, $e\in H$ and $e' \in f(H)$.
(inverse element) Pick any $f(x)$ from $f(G)$. Because $x^{-1} \in G$, $f(x^{-1}) = f(x)^{-1} \in f(G)$ which is the inverse of $f(x)$.
7. Preimage of a subgroup is a subgroup.
pf) Let $H'$ be a subgroup of $G'$ and $H_0 = f^{-1}(H')$.
(closedness) Pick any $x, y \in H_0$. Because $f(x) \in H'$, $f(y) \in H'$ and $H'$ is a subgroup of $G'$, $f(xy) = f(x)f(y) \in H'$. By definition of preimage, $xy \in H_0$.
(identity element) Because $e' \in H'$, $e \in \ker f \subseteq H_0$.
(inverse element) Pick any $x \in H_0$. Because both $f(x)$ and $f(x^{-1})$ are in $H'$, $x^{-1} \in H_0$.
8. $\ker f \subseteq H \le G \Rightarrow f^{-1}(f(H)) = H$.
pf) $f^{-1}(f(H)) \supseteq H$: Trivial.
$f^{-1}(f(H)) \subseteq H$: Let $x \in f^{-1}(f(H))$ which means $f(x) \in f(H)$. Suppose $x \notin H$. Then $\exists h \in H$ s.t. $f(x) = f(h)$. Because $f$ is a group homomorphism,
\begin{align}
e &= f(h)f(h^{-1}) \\
&= f(x)f(h^{-1})\\
&= f(xh^{-1})
\end{align}
Therefore $xh^{-1} \in \ker f \subseteq H$ which contradicts with the assumption that $x\notin H$.