hgtransform을 이용하여 이미지 회전시키기

매트랩으로 시각화 예제를 만들면서 이미지를 회전시켜야 할 일이 있었다. 하나의 Axes 위에 다른 객체는 그대로 놔두고 Image object만 회전시켜야 했는데, 정보 손실이 없어야 해서 imrotate는 사용하기 어려운 상황이었다. 찾아보니 rotate라는 함수가 Image object도 회전시킨다고 나왔다. 그런데 막상 해보니까 안되는 거다. 그래서 어쩔 수 없이 Axes를 2개 만들어서 Image를 올린 Axes만 회전시켰다.
해당 이슈를 매트랩 단톡방에 공유했고, 도움말에 오류가 있는 것으로 판명이 났다. 정식으로 이슈 등록되었고, Answers에 Support team의 글도 올라왔다. 요컨대 Image object에는 ZData가 없기 때문에 안된다고 한다. 지금은 rotate 함수의 설명에 Image object는 지원하지 않는다는 문구가 추가되어 있다.

방법이 없지는 않다. 위 링크에도 있듯이 hgtransform과 makehgtform을 이용하면 이미지를 회전시킬 수 있다. hg는 handle graphics의 약자인 듯 하다. hgtransform 함수는 Transform 객체를 만든다. Transform 객체는 Image, Line 등을 담을 수 있는 컨테이너다. Transform 객체의 Parent는 Axes다. 즉, Axes와 하위 그래픽 객체들 사이에 Transform 객체가 끼어들어간 것으로 볼 수 있다.
Transform 객체의 Matrix 속성에는 4x4 transform matrix가 들어 있다. 4x4인 이유는 translation도 하기 위함이다. 자세한 내용은 이 페이지를 참고하자. Matrix 속성을 바꾸어 Transform 객체에 담긴 그래픽 객체들을 한번에 rotation, translation, scaling을 할 수 있다. Matrix 속성에 들어갈 4x4 matrix를 만들어주는 함수가 makehgtform이다.
예를 들어, 아래와 같이 이미지를 Transform 객체인 ht1에 올리고, (hgtransform은 현재 Axes에 들어간다. Axes가 없으면 새로 만든다.)
ht1 = hgtransform();
cam = imread('cameraman.tif');
im1 = imagesc(ht1, cam); colormap gray
Line 객체를 추가한 후에 ht1.Matrix를 수정하면,
hold on,
plot(ht1, 1:256, 128 + 128*sin((1:256)*2*pi/256), 'r', linewidth=5)
ht1.Matrix = makehgtform('xrotate', pi/4);
view(3)
아래와 같이 ht1이 x축을 중심으로 회전한다.

이 상태에서 ht1에 다른 Line을 추가하면 회전한 상태로 추가된다. Parent인 Transform의 속성을 그대로 따르기 때문이다.
plot(ht1, 1:256, 128 + 128*cos((1:256)*2*pi/256), 'b', linewidth=5)

하나의 Axes 위에 여러 개의 Transform 객체가 올라갈 수 있다. 새로운 Transform 객체를 만들고,
ht2 = hgtransform();
이번엔 peppers.png를 올리고 z축으로 회전시켜보자.
pep = imread('peppers.png');
im2 = imagesc(ht2, pep);
ht2.Matrix = makehgtform('zrotate', pi/4);

어떤 그래픽 객체는 Transform 객체 위에 바로 올릴 수 없다. FunctionLine이나 viscircles는 Axes 위에만 올릴 수 있다. 하지만 방법이 있다. 일단 만든다.
fl = fplot(@(t) 100*sawtooth(t/10), [0, 256], 'g', LineWidth=5);
v = viscircles([100, 100], 100, Color='m');
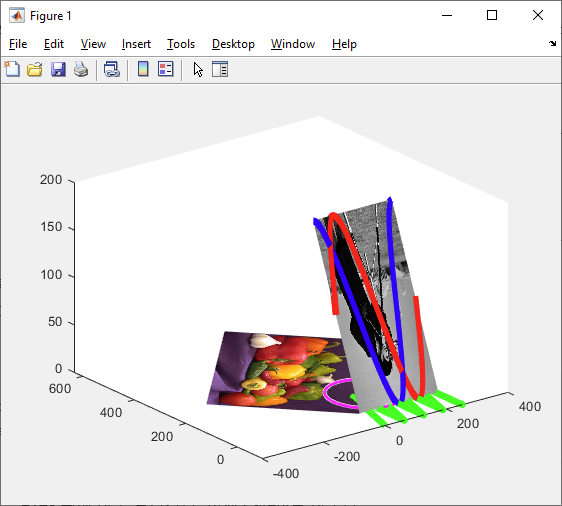
이 두 객체는 Axes 위에 바로 올라간다. 이제 Parent를 바꾼다.
fl.Parent = ht2;
v.Parent = ht1;
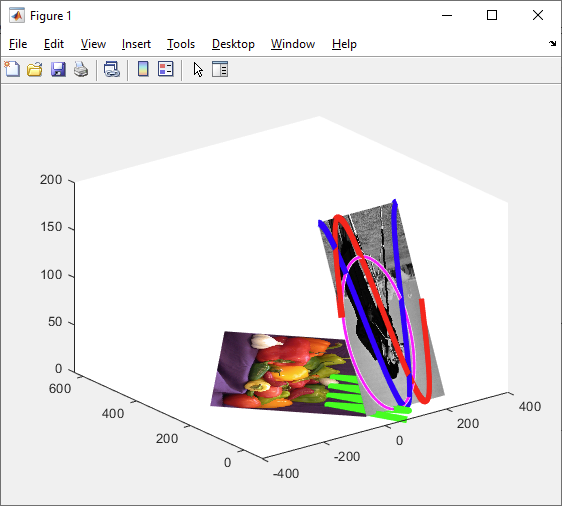
잘 된다.
makehgtform에는 scaling, rotation, translation을 한번에 넣을 수 있는데, 뒤에 들어간 것부터 적용됨에 주의해야 한다. 예를 들어 x 방향으로 1만큼 움직이고 z 축으로 90도 회전하고 싶다면 아래처럼 써야한다.
ht.Matrix = makehgtform('zrotate', pi/2, 'translate', [1, 0, 0]);
변환행렬을 이용하는 이유는 scaling, rotation, translation을 선형변환으로 다루기 위함이다. 현재 객체를 변환하고 싶다면 새로운 변환행렬을 현재 변환행렬의 앞에 곱해야 한다. 예를 들어 현재 상태에서 x 축으로 45도 회전하고 싶다면,
ht.Matrix = makehgtform('xrotate', pi/4) * ht.Matrix;
라고 써야 한다. 순서가 바뀌면 안된다. 행렬은 교환법칙이 성립하지 않기 때문이다. 함수로서의 선형변환을 생각하면 된다.
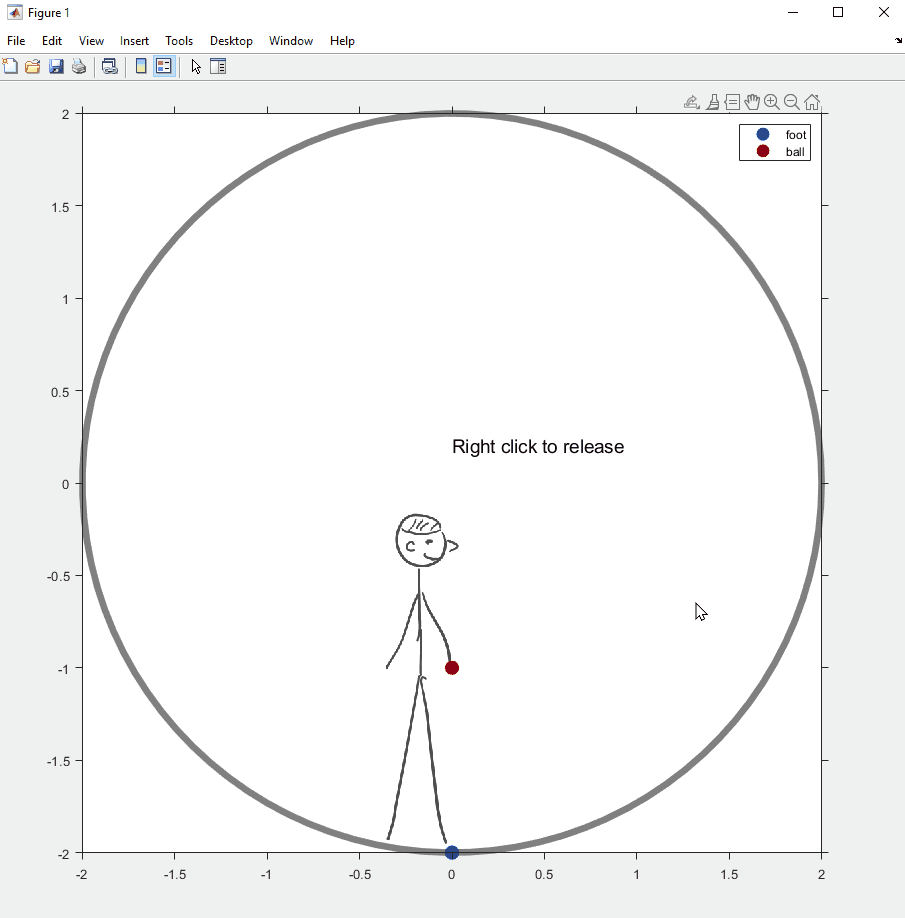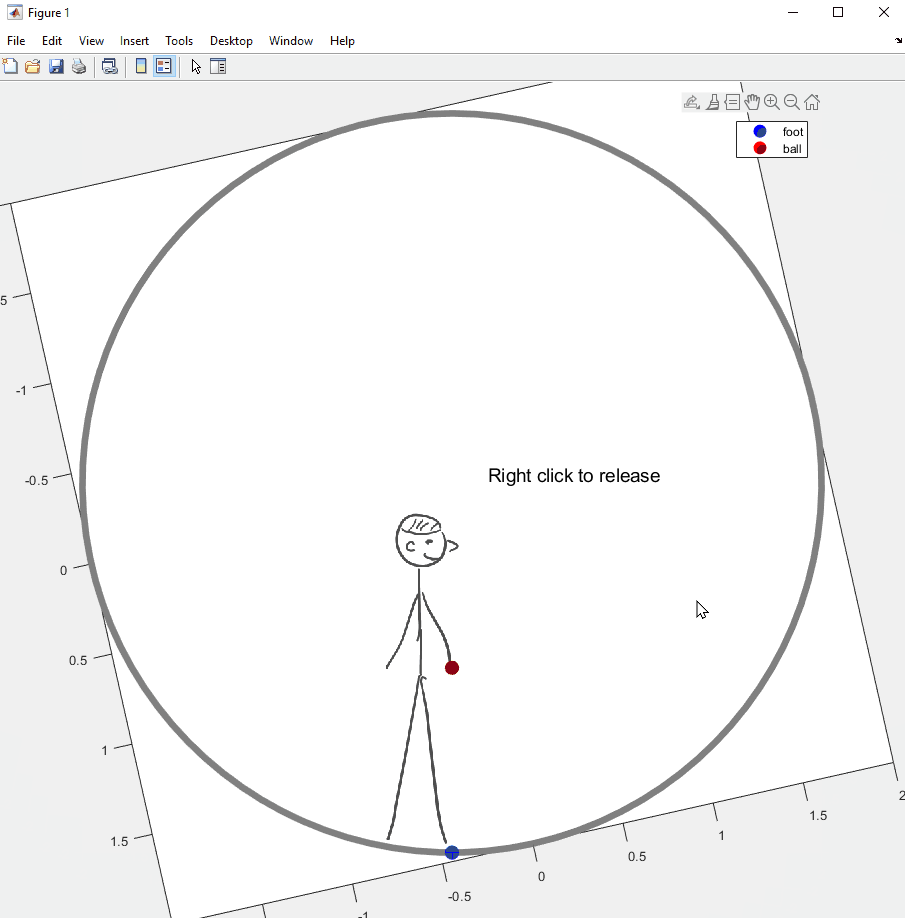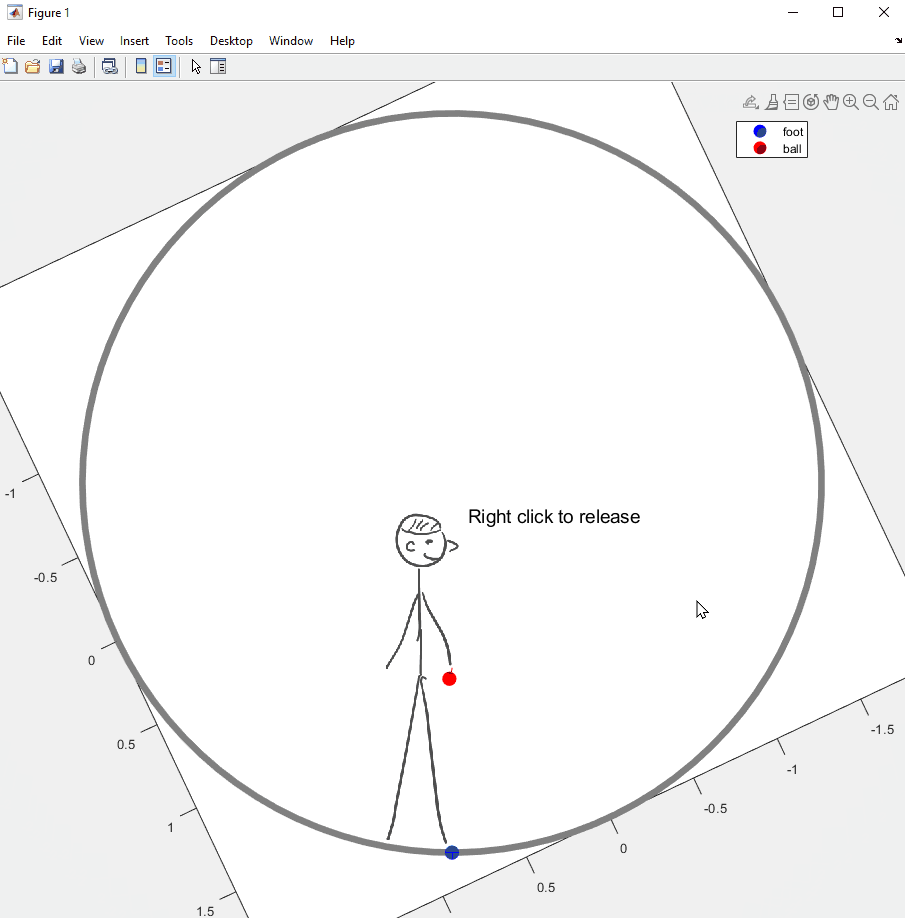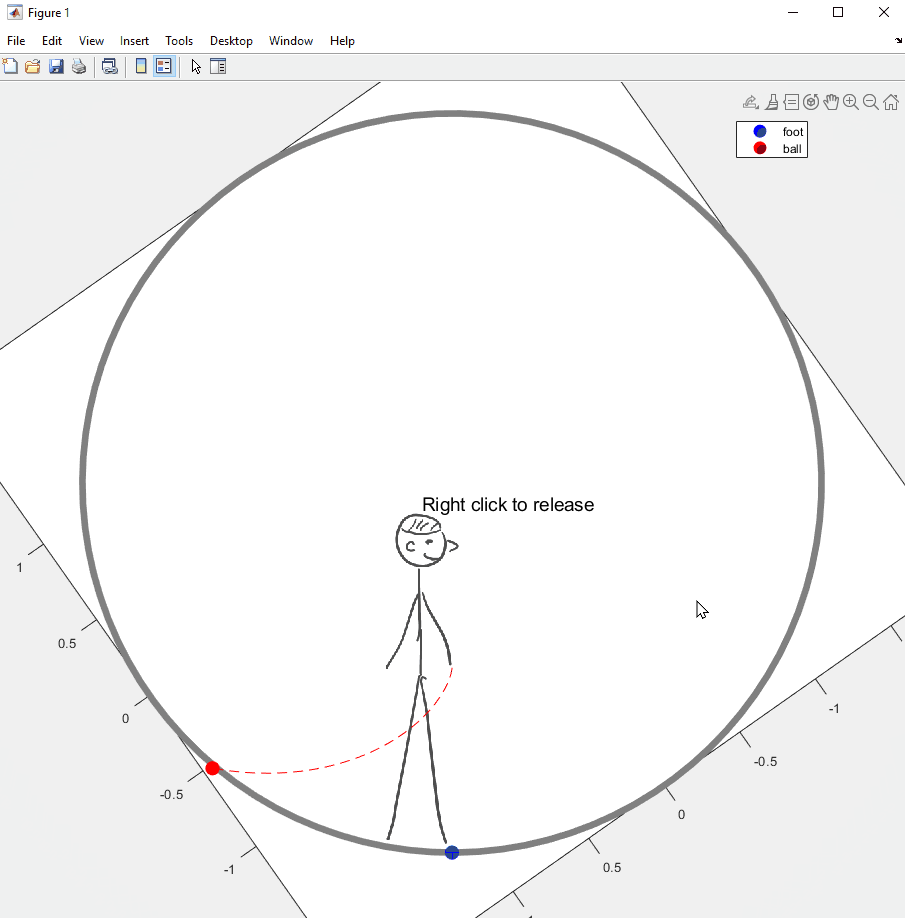
아래는 이 글 맨 앞에 썼던, 이미지를 회전시켜야 했던 시각화 예제의 코드와 결과물이다. 회전하는 우주선 안에서 들고 있던 공을 놓았을 때 공의 궤적이 어떻게 보이는지를 설명하기 위한 예제였다. 이미지를 가져오는데에 1-2초 정도 소요되니 불편하더라도 양해를...
clear
close all
clc
rotate_frame = true;
R = 2; % 우주선 반경
r = 1; % 센터에서 공까지 거리
w = 10; % 우주선 회전 각속도
dt = 0.005; % 시간 간격
q = linspace(0, 2*pi);
figure, ax = axes;
[mark, ~, alpha_mark] = imread('https://drive.google.com/uc?export=view&id=1-0RETRicKOp1FdfQv-Li8wBCiv2qB966');
mark = flipud(mark);
alpha_mark = flipud(alpha_mark);
h = imshow(mark);
h.AlphaData = alpha_mark;
ax.YDir = 'normal';
ht = hgtransform();
h.Parent = ht;
ht.Matrix = makehgtform('translate', [-R, -R, 0], 'scale', 2*R/size(mark,1));
hold on, box on,
axis equal tight vis3d on
ax.XLim = [-R, R];
ax.YLim = [-R, R];
% 우주선 테두리
plot(R*cos(q), R*sin(q), '-', ...
LineWidth=5, ...
Color=[.5, .5, .5], ...
HandleVisibility='off')
% 발
foot = plot(0, -R, 'bo', ...
MarkerFaceColor='b', ...
MarkerSize=10);
% 공
ball = plot(0, -r, 'ro', ...
MarkerFaceColor='r', ...
MarkerSize=10);
% 공 궤적
trajectory = plot(0, -r, 'r--');
text(0, 0.2, 0, 'Right click to release', ...
FontSize=14);
legend('foot', 'ball')
is_ball_in = @() norm([ball.XData, ball.YData])<=R;
pause(0.5)
% 우클릭 해야 공 놓음
iq = -pi/2;
while ~strcmp(get(gcf, 'SelectionType'), 'alt')
iq = iq + dt*w;
ball.XData = r*cos(iq);
ball.YData = r*sin(iq);
foot.XData = R*cos(iq);
foot.YData = R*sin(iq);
ht.Matrix = makehgtform('zrotate', dt*w) * ht.Matrix;
if rotate_frame
ax.View = [rad2deg(iq+pi/2), 90];
end
pause(0.05)
end
trajectory.XData = ball.XData;
trajectory.YData = ball.YData;
v_ball = 1i*w*(ball.XData + 1i*ball.YData);
v_ball = [real(v_ball), imag(v_ball)];
while is_ball_in()
iq = iq + dt*w;
ball.XData = ball.XData + dt*v_ball(1);
ball.YData = ball.YData + dt*v_ball(2);
foot.XData = R*cos(iq);
foot.YData = R*sin(iq);
% 사람 관점에서 공 궤적 계산
[traj_x, traj_y] = rotate2d(trajectory.XData, trajectory.YData, dt*w*rotate_frame);
trajectory.XData = [traj_x, ball.XData];
trajectory.YData = [traj_y, ball.YData];
ht.Matrix = makehgtform('zrotate', dt*w) * ht.Matrix;
if rotate_frame
ax.View = [rad2deg(iq+pi/2), 90];
end
pause(0.05)
end
function [x, y] = rotate2d(x, y, q)
xy = [
cos(q), -sin(q);
sin(q), cos(q)
]*[x;y];
x = xy(1, :);
y = xy(2, :);
end
끗
