수학에서의 역설
0. 들어가며
수학에서 역설은 흥미로운 주제이다. 듣다 보면 "이게 뭐지...?" 싶은데, 말이 되면서 동시에 말이 안되는 모순을 일으킨다. 그래서 흥미롭다. 생각할 거리를 주기 때문이다. 물론 흥미에서 끝나면 안되고, 해결을 해야 한다.
• 그렐링-넬슨의 역설
• 도서관 사서의 역설
• 이발사의 역설
• 베리의 역설
• 러셀의 역설
• 거짓말쟁이의 역설
이것들은 모두 다른 형태를 띠고 있지만, 곰곰이 따져보면 같거나 비슷한 명제의 다른 표현임을 알 수 있다.
주의: 이 글을 읽다보면 반복되는 단어에 정신이 혼미해질 수 있음
1. 그렐링-넬슨의 역설 (Grelling–Nelson paradox)
• 자기서술적인(Autological) 단어는 단어의 의미가 스스로를 설명하는 단어이다.
• '짧다'는 짧다. 그래서 '짧다'는 자기서술적이다.
• 비자기서술적인(Heterological) 단어는 단어의 의미가 스스로를 설명하지 못하는 단어이다.
• '길다'는 길지 않다. 그래서 '길다'는 비자기서술적이다.
• '한글'은 한글이므로 자기서술적이다. '영어'는 영어가 아니므로 자기서술적이지 않다.
• 그렇다면 '비자기서술적'은 비자기서술적인가?
• '비자기서술적'이 비자기서술적이라면 스스로를 설명하고 있으므로 자기서술적이어야 한다.
• '비자기서술적'이 자기서술적이라면 자기를 서술하므로 비자기서술적이어야 한다.
• 즉, 어느 답을 해도 모순이 된다.
• 뭔가 말장난에 속는 느낌이라면 이렇게 생각해보자.
• 이 질문의 답은 "그렇다" 또는 "아니다" 둘 중 하나여야 한다.
• "짧다"는 짧다. $\Longleftrightarrow$ "짧다"는 자기서술적이다. (자)
• "길다"는 길지 않다. $\Longleftrightarrow$ "길다"는 비자기서술적이다. (비)
• 만약 "비자기서술적"이 비자기서술적이라면?
• "비자기서술적"은 비자기서술적이다.
• (비)에 의해 "비자기서술적은" 비자기서술적이 아니다. (모순)
• 만약 "비자기서술적"이 비자기서술적이지 않다면?
• "비자기서술적"은 자기서술적이다.
• (자)에 의해 "비자기서술적"은 비자기서술적이다. (모순)
• 즉, '비자기서술적'은 비자기서술적이라고 해도 모순이고 비자기서술적이지 않다고 해도 모순이다.
• 사실 '자기서술적'도 문제이다.
• '자기서술적'은 자기서술적이라고 해도 말이 되고, 자기서술적이 아니라고 해도 말이 된다.
2. 도서관 사서의 역설 (The librarian paradox)
• 어떤 도서관에 소설도 있고 시집도 있고 수학책도 있고 과학책도 있다.
• 이 도서관의 사서가 책들의 카탈로그를 만들기로 했다.
• 소설과 시집의 카탈로그를 각각 C1, C2라고 이름 붙였다.
• 그리고 특이하게도, C1, C2에는 자신의 이름도 들어 있다.
• 수학책과 과학책의 카탈로그는 각각 C3, C4라고 이름 붙였다.
• 이것들에는 자신의 이름을 쓰지 않았다.
• 이제 마지막으로 카탈로그의 카탈로그를 두 권 만들었다.
• A에는 자기 자신을 적은 카탈로그들을, B에는 자기 자신을 적지 않은 카탈로그들을 적었다.
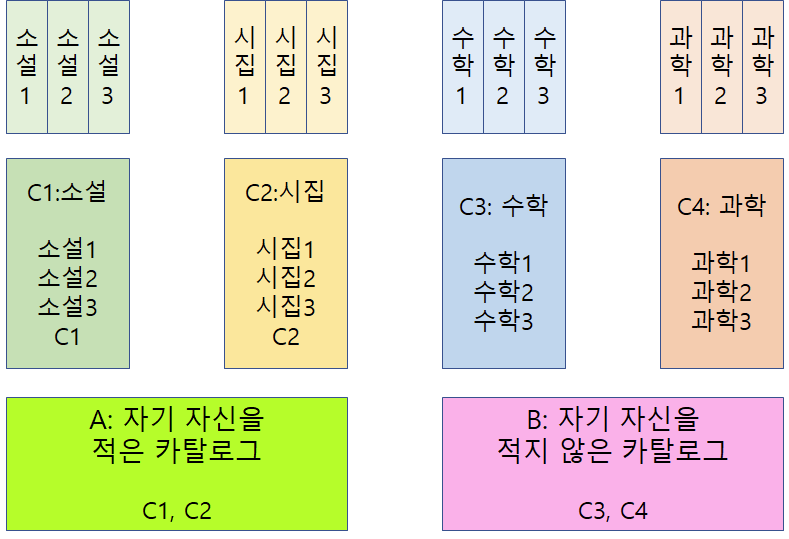
• 그런데 A와 B도 카탈로그이다.
• A와 B도 A 또는 B에 들어가야 한다.
• A는 어디에 적든 말이 된다.
• B는 어디에 적어도 모순이다.
• B를 A에 적으면 B에는 자신이 적혀있지 않으므로 모순이다.
• B를 B에 적으면 B에 자신이 적혀 있으므로 모순이다.
• 사실상 Autological/Heterological과 같은 문제이다.
3. 이발사의 역설 (Barber's paradox)
• 어떤 마을에는 두 분류의 사람들이 있다.
• 셀프 면도하는 사람들이 있다. 이들은 자기 자신만 면도한다. 남을 해주지도 않고, 남이 해주지도 않는다.
• 셀프 면도를 못하는 사람들도 있다. 이들은 누군가 면도를 해줘야 한다.
• 이 마을에는 이발사가 딱 한 명 존재한다.
• 이발사는 셀프 면도를 못하는 사람들만, 모두, (all and only) 면도해준다. 셀프로 하는 사람은 해주지 않는다.
• 이 이발사는 셀프 면도하는가?
• 이발사가 셀프 면도하려면, 셀프 면도하는 사람은 해주지 않아야 하므로, 셀프 면도를 하지 말아야 한다.
• 이발사가 셀프 면도하지 않으려면, 셀프로 못하는 사람은 자기가 해줘야 하므로, 셀프 면도를 해야 한다.
• 역설들 중에서 이게 제일 복잡하다.
• 문제 세팅도 조심해서 해야 하는데, 이발사가 셀프 면도 못하는 사람들을 전부(all), 그들만(only) 해줘야 한다.
• 그래서 "이렇게 저렇게 하면 해결되는거 아니냐"라는 지적이 많다.
• 요지는 "이렇게 저렇게" 바꾸지 않으면 모순이 해결되지 않는다는 점이다.
• 이 링크를 보면 "이발사가 딱 한 명 존재한다"는 전제를 꼭 깔아야 한다고 한다.
• 그렇지 않으면 "이발사가 존재하지 않음(공집합의 비존재성)"으로서 모순이 해결되어 버리기 때문이다.
4. 베리의 역설 (Berry's paradox)
• 1은 "일"이라는 한 글자로 정의할 수 있다.
• 51672569는 "오천백만육십칠만이천오백육십구"라는 열 다섯 글자로 정의할 수도 있지만
• "이천이십이년대한민국인구수"라는 열 세 글자로 정의할 수도 있다.
• 숫자를 정의하는 방법은 여러 가지 있을 수 있는데, 그 중 가장 짧은 것만 택한다.
• 물론 숫자가 아주 커지면 더 많은 글자가 필요할 것이다.
• 모든 자연수를 "스무 글자 이하로 정의할 수 있는 자연수"와 "스무 글자 이하로 정의할 수 없는 자연수"로 나누자.
• 스무 글자 이하로 정의할 수 있는 자연수는 유한개이다.
• 따라서 스무 글자 이하로 정의할 수 없는 자연수 중 가장 작은 자연수가 분명히 존재할 것이다.
• "스무 글자 이하로 정의할 수 없는 가장 작은 자연수"는 둘 중 어디에 들어가야 하는가?
• "스무 글자 이하로 정의할 수 없는 가장 작은 자연수"는 정확히 스무 글자이다.
• 왼쪽에 넣으려 하니 "스무 글자로 정의할 수 없음"이라는 자기 설명에 모순이다.
• 오른쪽에 넣으려 하니 스스로를 스무 글자 이내로 정의했으므로 모순이다.
5. 러셀의 역설 (Russell's paradox)
• 집합 $X$는 자기 자신을 원소로 갖지 않는 집합들을 모두 모은 것이다.
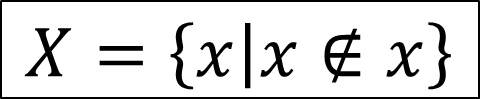
• 우선 집합이 자기 자신을 원소로 갖는다는 것이 무슨 말인지 알아야 한다.
• 집합 $A$를 "아이폰을 모두 모은 것"으로 정의하자.
• 집합 $B$는 "아이폰이 아닌 것을 모두 모은 것"으로 정의하자.
• 집합 $B$는 아이폰이 아니다. 따라서 $B$는 $B$의 원소이다.
• 위의 집합 $X$는 자기 자신을 원소로 갖는가? 갖지 않는가?
• 자신을 원소로 갖는다면, 자신을 원소로 갖지 않는 것들만 모았다는 정의에 모순이다.
• 자신을 원소로 갖지 않는다면, 역시 집합의 정의에 의해 자신을 원소로 가져야 해서 모순이다.
6. 거짓말쟁이의 역설 (Liar paradox)
• 아래의 명제를 보자.
• 명제 $P$는 참인가? 거짓인가?
• 참이라면, 스스로 거짓이라고 말하고 있으므로 거짓이다.
• 거짓이라면, 스스로 거짓임을 밝히고 있으므로 참이다.
7. 역설들의 형태
• 지금까지 나왔던 역설들을 모두 모아보자.
• 자세히 쳐다보면...
• 모두 같은 형태임을 알 수 있다.
[뭐뭐]하지 않은 것들의 집합은 [뭐뭐]한가?
([뭐뭐]한 집합에 속하는가?)
• 공통적으로 부정형의 집합이 자기 참조를 함으로 인해 발생하는 문제들이다.
• 재밌는 점은, 괴델의 불완정성 정리와 정지문제(Halting problem)에도 비슷한 형태가 보인다는 것이다.
• 괴델의 불완정성 정리에는 "나의 증명은 존재하지 않는다"라는 명제가 등장하며,
• 정지 문제에서는 기계의 설계도를 입력받아 기계가 멈출지를 판단하는 기계에 자신의 설계도를 입력한다.
8. 집합론의 공리계
• 이런 간단한 명제조차 참/거짓을 판단하지 못하는 사태가 벌어졌을 때, 수학자들이 단체로 멘붕했다고 한다.
• 그래서 이런 일이 생기지 않도록 집합론의 공리계를 만들었다.
• 가장 유명(?)한 것은 ZFC 공리계이다.
• ZFC에는 분류 공리(Axiom of Separation)이라는 것이 있는데, 원문(?)을 해석하자면 아래와 같다.
집합은 이미 존재하는 것들로만 만들 수 있다.
정의된 집합 밖에서 아무거나 가져와서 집합을 만들 수는 없다.
• 기초 공리(Axiom of Foundation) 또는 정칙성 공리(Axiom of Regularity)라고 부르는 것도 있다.
• 역시 해석하자면 아래와 같다.
공집합이 아닌 모든 집합은 자신과 서로 소인 원소를 갖는다.
자기 자신을 원소로 갖는 집합은 허용하지 않는다.
• 집합이 자신의 원소와 서로소라는 것이 다소 난해하다.
• 모든 것을 집합으로 보겠다는 말인 것 같다.
• 사실 무슨 말인지 잘 모르겠다.
• 암튼 러셀의 역설에 나오는 집합이 아예 집합이 아니도록, 그런 집합이 존재하지 않도록 공리로 못박아버렸다.
• ZFC 공리계 말고도 Type Theory도 있고, NBG(노이만-베르나이스-괴델) 공리계도 있다.
• 잘 모르니까 패스한다.
9. 마치며
• 언젠가 한번 정리하고 싶었던 내용인데 드디어 정리했다.
• 집합론은 너무 파지 말자.
끗.