역함수의 존재성과 전단사 함수에 대하여

(본 글은 수학의 즐거움 직문수 4강을 참고하여 작성한 것입니다.)
아래와 같은 함수 $f: A \to B$가 있다.

함수가 갖춰야 할 조건을 모두 갖췄으므로 분명히 함수가 맞다. $f: A \to B$의 역함수 $g: B \to A$는 아래 조건을 만족해야 한다.
$$g \circ f = \mathrm{id}_A$$
$$f \circ g = \mathrm{id}_B$$
$\mathrm{id}_A$와 $\mathrm{id}_B$는 각각 $A$에서 $A$로 가는 항등함수, $B$에서 $B$로 가는 항등함수를 말한다. 합성 함수의 결과가 항등함수가 되어야 한다고 하니, 그냥 심플하게 뒤집어서 붙여보자.

아차, $g$가 함수가 아니다. $g$가 함수이려면 어떻게 해야 할까? 우선 2와 3이 모두 $b$를 가리켜서는 답이 없다. $g(b)=2$이면 $g \circ f(3) \neq 3$이고, $g(b)=3$이면 $g \circ f (2) \neq 2$이기 때문이다. 따라서 $f$는 반드시 단사함수여야 한다.

이렇게...? 아차, $e$는 어떡하지? $g$가 함수이기만 하면 되니까 $e$는 아무데로나 쏘자.

이렇게 만든 함수 $g$는 분명히 아래를 만족한다.
$$g \circ f = \mathrm{id}_A$$
실제로는 아래 두 명제가 동치이다.
(1) 함수 $f: A \to B$가 단사함수이다.
(2) $g \circ f = \mathrm{id}_A$인 함수 $g: B \to A$가 존재한다.
이번엔 $f \circ g = \mathrm{id}_B$다. 이번에도 심플하게 뒤집어서 붙여보자.
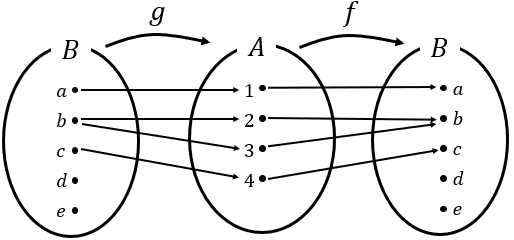
뭐가 문제가 많다. 우선 $d$와 $e$가 문제다. $d$를 $d$로, $e$를 $e$로 되돌려주면서 $f$가 함수이려면,
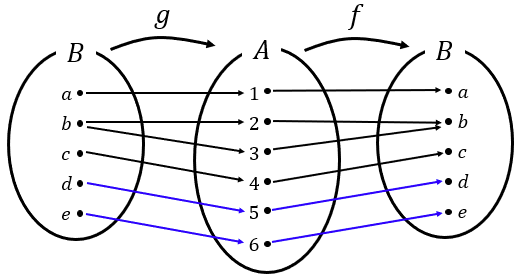
$f$가 이런 모양일 수밖에 없다. 즉, $f$는 반드시 전사함수여야 한다.
해결할 문제가 하나 더 남았다. $b$는 2와 3 둘 중 하나로만 가야 한다. 아무거나 고르자.
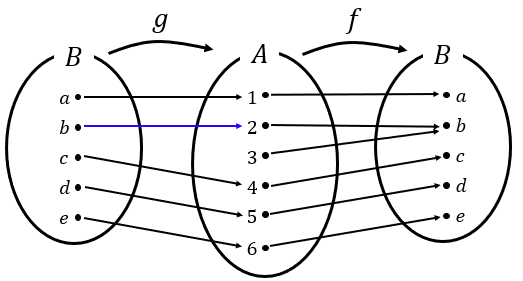
이렇게. 이 함수 $g$는 분명히 아래를 만족한다.
$$f \circ g = \mathrm{id}_B$$
실제로는 아래 두 명제가 동치이다.
(1) 함수 $f: A \to B$가 전사함수이다.
(2) $f \circ g = \mathrm{id}_B$인 함수 $g: B \to A$가 존재한다.
이걸로 다 된걸까...? 혹시...
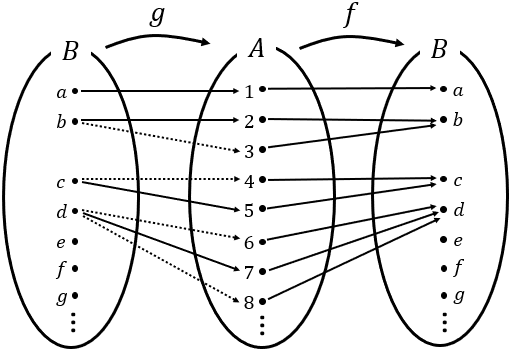
$b$를 2와 3 중 어디로 쏠지 골랐던 것처럼 골라야 하는 경우가 너무 많으면? 그 경우가 무한개라면? 무한개의 집합에서 원소를 하나씩 고르는 함수가 정말 잘 존재하는지 우리는 알 수 없다.
하지만 그런 함수가 존재한다고 치자. 이것을 선택공리Axiom of Choice, AoC라고 부른다.
선택공리는 너무 자명해보이기 때문에 왜 굳이 공리로 두어야 하는지 받아들이기 어려울 수 있다. 하지만 선택공리로부터 유도되는 유명하고 비직관적인 정리가 있다. 궁금하면 아래 영상을 보자.
(참고로 선택공리를 받아들이지 않는 수학자도 있다. 어디까지나 공리일 뿐이니까.)
어쨌든 결론은 아래와 같다.
함수 $f: A \to B$에 대해
$$g \circ f = \mathrm{id}_A$$
$$f \circ g = \mathrm{id}_B$$
를 만족하는 $f$의 역함수 $g: B \to A$가 존재하기 위한 필요충분조건은 $f$가 전단사 함수인 것이다.
- 게으른