n차원 구의 부피는?

n차원 구의 부피는 어떻게 계산할까요? 어...음... n차원 구가 무엇인지부터 말을 할 수 있어야겠군요.
3차원 구는 3차원 공간의 점들 중 어떤 한 점에서 떨어진 거리가 어떤 고정된 상수인 점들의 집합입니다. 3차원 단위구는 한 점에서 떨어진 거리가 1인 점들의 집합이죠. 그렇다면 2차원 구는 한 점에서 떨어진 거리가 어떤 고정된 상수인 2차원 공간의 점들의 집합이라고 볼 수 있겠군요. 네, 원입니다.

이 개념을 n차원으로 확장하지 못할 이유는 없습니다. n차원 구는 n차원 공간의 점들 중 어떤 한 점에서 떨어진 거리가 고정된 상수인 점들의 집합이고, n차원 단위구는 이 거리가 1인 점들의 집합일 겁니다.
2차원 구(원)의 부피는
$$ V(2) = \pi r^2 $$
이죠. 3차원 구의 부피는
$$ V(3) = \frac{4}{3} \pi r^3 $$
입니다. 오호라. 패턴이 보이는군요. n차원 구의 부피는 왠지 아래처럼 생겼을 것 같습니다.
$$ V(n) = c r^n $$
c는 어떤 상수일텐데, 이 상수가 n에 따라 어떻게 변할지가 궁금해집니다. 부피가 무엇인가에 대한 고민도 동반되어야 하긴 하겠으나, 수학 얘기는 자세히 하지 않겠습니다. 사실 저도 몰라요.
앞에서 '거리'라는 단어를 자연스럽게 사용했습니다. 사실 두 점 사이의 거리를 정의하는 방법도 한 가지가 아닙니다. 하지만 자연스럽게 은근슬쩍 유클리드 거리만 생각합시다.
$$d((x_1, x_2, ... x_n), (y_1, y_2, ... y_n)) = \sqrt{ \sum_{i=1}^{n} (x_i - y_i)^2 }$$
그렇다면 매트랩을 이용해서 n 차원 공간의 임의의 두 점 간의 거리를 계산 못할 이유도 없겠네요. 사실 이미 함수가 있습니다. norm을 이용하면 됩니다. (pdist도 있습니다.)
>> x = [1, 2, 3, 4];
>> y = [4, 3, 2, 1];
>> norm(x-y)
ans =
4.4721
>> sqrt(sum((x-y).^2))
ans =
4.4721
아하? 그렇다면 매트랩으로 n차원 구의 부피를 계산할 수 있을까요?
원주율을 계산하는 방법은 여러 가지가 있는데, 그 중 재밌는 방법을 하나 소개합니다. 몬테 카를로 시뮬레이션을 돌리는 건데... 자세한 내용은 아래 영상을 보시죠.
이 아이디어를 차용하도록 하죠. n차원 공간의 각 축 좌표가 $[-1, 1]$ 범위로 정의되는 어떤 공간을 생각해봅시다. 2차원이면 정사각형, 3차원이면 정육면체겠네요. 이 공간에 랜덤하게 점을 뿌리고 그 중 거리가 1보다 작은 점의 개수를 세어보는 겁니다.
order = 1:23; % 2^order개만큼의 점을 생성
ndim = 4; % 4차원
vol_ndim = zeros(size(order));
for n=1:length(order)
N = 2^n; % 전체 점 개수
r = rand([N, ndim])*2 - 1; % ndim 차원에 점 생성
radius = vecnorm(r');
vol_ndim(n) = sum(radius<=1)/N*2^ndim;
fprintf('vol. of %2d-dim sphere (2^%d points) = %6.4f R^%d\n', ...
ndim, n, vol_ndim(n), ndim)
end
vecnorm은 2차원 행렬의 각 column의 norm을 계산하는 함수입니다. 위 코드처럼 for문을 통해 n차원 공간에 뿌릴 점의 개수를 점점 늘려가면 언젠가 단위구에 들어간 점의 비율이 수렴하지 않을까요?
plot(order, vol_ndim)
xlabel('dimension')
ylabel('ratio of points with dist<=1')
set(gca, 'FontSize', 14)
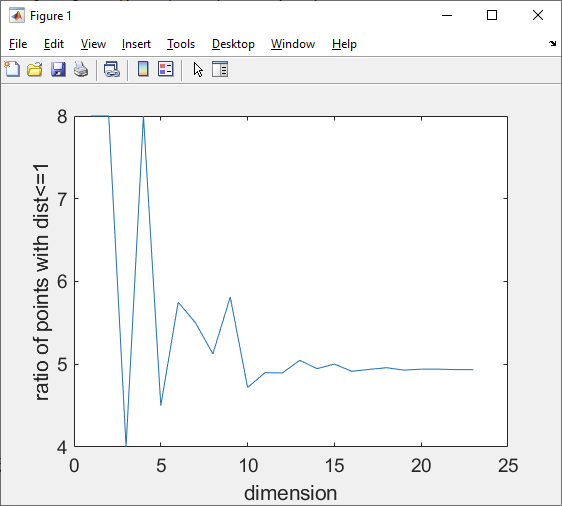
수렴했네요. 수렴값은 4.934 정도입니다. 같은 방식으로 5, 6, 7차원에 대해 코드를 돌려봤더니,
$$ V(4) \cong 4.9342 r^4$$
$$ V(5) \cong 5.2686 r^5$$
$$ V(6) \cong 5.1727 r^6$$
$$ V(7) \cong 4.7218 r^7$$
라는 값들이 나왔군요. 사실 정확한 값이 이미 계산되어 있습니다. 아래는 위키피디아에 나온 표입니다.
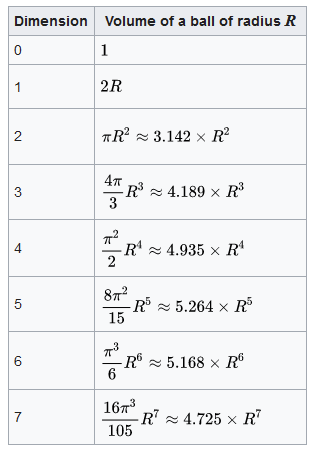
매트랩 계산 결과와 꽤 비슷한 값이 나왔습니다. 점을 더 많이 찍으면 더 정확한 값이 나오겠으나, 정확한 값이 있는데 굳이 그럴 필요는 없겠습니다. 단지 이 방식이 동작한다는 걸 확인했으면 충분한거죠.
- 게으른