e의 정의

지수함수의 도함수
일단 임의의 양의 실수 $a$에 대해 지수함수 $y=a^x$는 $x\in\mathbb{R}$에서 잘 정의된다고 치자. 또한 그래프가 어떻게 생겼는지도 알고, 몇 가지 성질도 이미 주어져있다고 치자. ($a^0=1, a^1=1, a^{p+q}=a^p \cdot a^q, a^{pq}=\left(a^p\right)^q, a^{-p}=1/a^p$, 치역, 연속, 단조증가함수 등)
이제 $y=a^x$의 도함수를 계산해보자.
$$\begin{align}\frac{df}{dx}&= \lim_{h\to0}{\frac{a^{x+h}-a^x}{h}} \\
&= a^x \lim_{h\to0}{\frac{a^{h}-1}{h}} \\
&=\lambda a^x \\
&=\lambda f(x) \tag{1}
\end{align}$$
여기서 $\lambda$는 아래와 같이 정의되는 상수이며, 도함수의 정의에 의해 $y'(0)$이다.
$$\lambda = \lim_{h\to0} {\frac{a^h-1}{h}} = y'(0)\tag{2}$$
식 (1)을 보면 지수함수는 특별한 함수임을 알 수 있다. 도함수가 자기 자신의 상수배가 된다. 그렇다면 $\lambda=1$이라면 매우 특별한 함수일 것이다. 매우 특별한 것이니 이름을 붙이자. 아래 식을 만족하는 실수 $a$를
$$1 = \lim_{h\to0} {\frac{a^h-1}{h}}$$
지수함수(exponential)를 대표한다는 의미로 $e$라고 표기하자.
$$1 = \lim_{h\to0} {\frac{e^h-1}{h}}\tag{3}$$
그렇다면 $y=e^x$의 $x=0$에서의 기울기는 1이다.
지수함수의 역함수
한편 $y=a^x$는 단조증가함수이므로 역함수를 생각할 수 있다. $y=a^x$의 역함수는 $x=a^y$를 만족할 것이다. 이것을 $y$에 대한 explicit form으로 쓰기위해 아래와 같은 함수 $\log$를 정의하자.
$$y=\log_ax \Leftrightarrow x=a^y\tag{4}$$
우리말로 풀어 쓰자면 $\log_ax$는 "$a$를 몇 승하면 $x$가 되는가"라고 말할 수 있을 것이다. $y=a^x$와 $y=\log_ax$를 그래프로 그리면 아래와 같을 것이며,
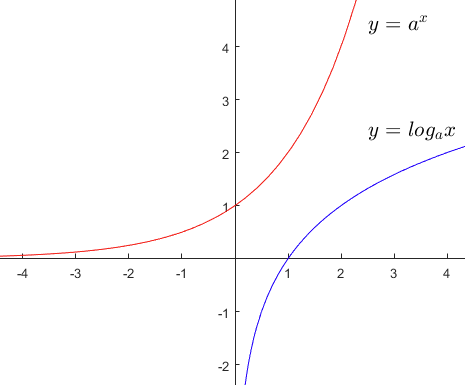
두 그래프는 역함수 관계이므로 $y=x$ 그래프에 대해 대칭이며, $y=a^x$의 $x=0$에서의 기울기와 $y=\log_ax$의 $x=1$에서의 기울기도 역수 관계일 것이다. 이 값을 계산해보자.
\begin{align}
1 &= \lim_{h\to0}{\frac{e^h-1}{h}} \\
&= \lim_{h\to0}{\frac{e^{h \log_ea}-1}{h \log_ea}} \\
&= \lim_{h\to0} \frac{1}{\log_ea}{\frac{a^{h}-1}{h}} \\
&= \frac{1}{\log_ea} \cdot \lim_{h\to0} {\frac{a^{h}-1}{h}} \\
&= \frac{1}{\log_ea} \cdot \frac{d}{dx}a^x \Biggr|_{x=0}
\end{align}
로부터
\begin{align}
\frac{d}{dx}a^x \Biggr|_{x=0} &= \log_ea\\
\frac{d}{dx} \log_ax \Biggr|_{x=1} &= \frac{1}{\log_ea}
\end{align}
임을 알 수 있다. $a=e$라면 특별히
\begin{align}
\frac{d}{dx}e^x \Biggr|_{x=0} &= \log_ee=1\\
\frac{d}{dx} \log_ex \Biggr|_{x=1} &= \frac{1}{\log_ee}=1 \tag{5}
\end{align}
이 되어, $y=e^x$의 $x=0$에서의 기울기와 $y=\log_ex$의 $x=1$에서의 기울기는 1로 같다.
$\log$ 함수의 성질
$\log$ 함수에는 재밌는 성질이 있다. 임의의 양의 실수 $x$와 임의의 실수 $y$에 대해서
$$\log_a x^y = y \log_ax\tag{6}$$
가 성립한다. 증명은 아래와 같다.
\begin{align}
z &= \log_a x^y \\
a^z &= x^y \\
a^{z/y} &= x \\
\log_a a^{z/y} &= \log_a x \\
\frac{z}{y} &= \log_ax \\
z &= y \log_ax
\end{align}
$e$의 정의
이제 $e$ 값을 (3)과 같은 형태가 아닌 explicit form으로 정의해보자. 식 (3)과 (5)로부터
$$1= \lim_{h\to0} \frac{e^h-1}{h} = \lim_{h\to0} \frac{\log_e (1+h)}{h}$$
이고, 식 (6)으로부터
$$1= \lim_{h\to0} \frac{\log_e (1+h)}{h} = \lim_{h\to0} \left[ {\log_e (1+h)}^{\frac{1}{h}}\right]$$
이다. $\log_ex$는 $x$에 대한 연속함수이므로
$$1= \lim_{h\to0} \left[ {\log_e (1+h)}^{\frac{1}{h}}\right] = \log_e \left[{\lim_{h\to0} { (1+h)}^{\frac{1}{h}}}\right]$$
가 성립하며, $\log$ 함수의 정의에 의해
$$e = \lim_{h\to0} { (1+h)}^{\frac{1}{h}} $$
이다.
$e$의 다른 정의
$e$를 정의하는 다른 방법도 있다. 우선 $y=e^x$의 $x=x_0$에서의 기울기는 $e^{x_0}$이다. $\log$ 함수는 지수함수의 역함수이므로, $y=\log_ex$의 $y=y_0$에서의 기울기는 $1/e^{y_0}$일 것이다. $y_0=\log_ex_0$로 두면 $e^{y_0} = x_0$이므로, $y=\log_ex$의 $x=x_0$에서의 기울기는 $1/x_0$가 된다.
$$\frac {d}{dx} \log_ex = \frac{1}{x}$$
양변을 1에서 $a(>1)$까지 적분해보자.
$$\int_1^a \frac{d}{dx} \log_ex \hspace{1mm}dx = \log_ea - \log_e1 = \log_ea = \int_1^a \frac{1}{x} \hspace{1mm}dx$$
이 되며, 특별히 $a=e$일 때
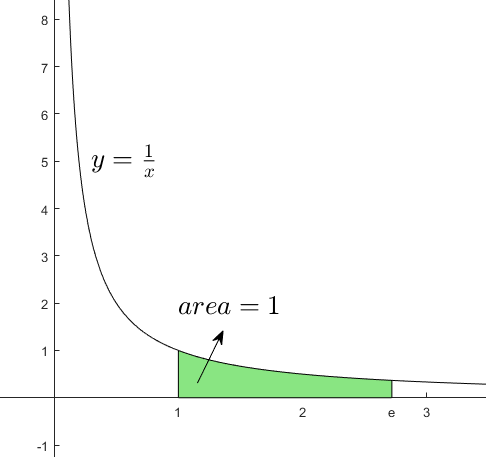
$$1= \int_1^e \frac{1}{x} \hspace{1mm}dx$$
가 된다. 즉, $e$는 $x=1, x=e, y=0, y=1/x$ 그래프로 둘러싸인 면적이 1이 되게 하는 상수이다.
게으른