입델 그런거 왜 함?
극한을 배웠다면 숨쉬듯이 당연하게 느껴지는 아래 식을 봅시다.
$$\lim_{x \rightarrow \infty} \frac{1}{x}=0$$
당연해보이나요? 질문을 하나 해보죠. $1/x$이 $0$이 될 수 있나요? $x$가 무한대이면 되지 않냐고요? 무한대가 뭔가요? 정의할 수 있나요? 정의할 수 있다고 쳐보죠. $1/\infty =0$인 어떤 수 $\infty$가 존재한다고 칩시다. 그런데 어떤 수든 $0$과 곱하면 $0$이 됩니다. 따라서 $1 = 0\times\infty = 0$으로부터 $0=1$이라는 해괴망측한 결론이 도출됩니다.
따라서 $1/x$은 절대 $0$이 될 수 없습니다. 그럼 위 극한식이 의미하는 바는 뭘까요?
문제의 가장 큰 원인은 잘 정의되지 않는 '무한'이라는 단어를 우리가 너무 쉽게 쓰고 있다는 점입니다. 고등학교 때까지는 위 식을 아래처럼 말합니다.
"$x$가 무한히 커지면 $1/x$은 0에 무한히 가까이 간다."
$x$가 얼마나 커져야 무한히 커졌다고 말할 수 있나요?
$1/x$이 얼마나 작아져야 $0$에 무한히 가까워졌다고 말할 수 있나요?
앞에서 말했듯이 '무한'은 쉽게 정의하기 어려운 개념입니다. 따라서 극한을 말하는 법을 바꿔야 합니다. '무한'이 문제라고 하니, '무한'을 빼고 말해보죠. 우선 '$x$가 무한히 커진다'는 '어떤 양수를 잡아도 $x$는 그것보다 크다' 정도로 말할 수 있을 것 같습니다. $1/x$이 $0$에 무한히 가까이 간다? 아마 이 말을 하고 싶었을 겁니다.
"$1/x$을 얼마든지 원하는 만큼 $0$에 가깝게 만들 수 있다."
'원하는 만큼 $0$에 가깝게'라는 표현에도 '무한'의 개념이 녹아있는 것 같습니다. 바꿔보죠.
"아무리 작은 양의 실수 $\epsilon$을 잡아도, $1/x$를 $\epsilon$보다 작게 만들 수 있다."
'아무리'라는 표현도 애매하군요.
"어떤 양의 실수 $\epsilon$에 대해서도 $1/x$를 $\epsilon$보다 작게 만들 수 있다."
'어떤 양의 실수 $\epsilon$에 대해서도'를 좀 더 수학적으로 표현할 방법이 있습니다.
"임의의 양의 실수 $\epsilon$에 대해서 $1/x$를 $\epsilon$보다 작게 만들 수 있다."
'만들 수 있다'는 '존재한다'로 바꿔도 될 것 같습니다.
"임의의 양의 실수 $\epsilon$에 대해서 $0<1/x<\epsilon$인 실수 $x$가 존재한다."
어떤가요? 무한의 개념은 1그람도 들어있지 않습니다. 이제 극한의 정의가 제대로 된 것 같습니다.
아르키메데스 성질(Archimedean property)이라는 것이 있습니다. 나무위키에 이렇게 써있네요.
이게 무슨 말일까요? 이제 우리는 이 표현을 해석할 준비가 되어 있습니다.
자연수 $N$이 존재한다. $\rightarrow$ 자연수 $N$을 찾을 수 있다.
임의의 양의 실수 $\epsilon$에 대해 $\rightarrow$ 아무리 작은 양의 실수 $\epsilon$에 대해서도
임의의 $M\in\mathbb{R}$에 대해 $\rightarrow$ 아무리 큰 실수 $M$에 대해서도 (음수여도 상관없지만 여기서는 패스)
하나로 합쳐볼까요?
"아무리 작은 양의 실수 $\epsilon$과 아무리 큰 실수 $M$에 대해서도 $N\epsilon>M$을 만족하는 자연수 $N$을 찾을 수 있다."
아주 살짝만 리터치를 해보죠.
"아무리 작은 양의 실수 $\epsilon$과 아무리 큰 실수 $M$에 대해서도 $\epsilon/M>1/N$을 만족하는 자연수 $N$을 찾을 수 있다."
$x\rightarrow\infty$일 때 $1/x$의 극한값의 정의와 굉장히 비슷하지 않나요? 사실 거의 같은 개념을 말하고 있는 것입니다.
위 예시는 $x$가 무한대로 갈 때 $1/x$이 $0$이 되는 경우였습니다. 이걸 일반화해서, $x$가 어떤 값 $a$로 가까이 갈 때 함수 $f(x)$의 값이 $L$에 가까이 간다는 것을 수식으로 아래처럼 표시합니다.
$$\lim_{x \rightarrow a} f(x) = L$$
이것도 무한의 개념을 쓰지 말고 표현해보겠습니다. 아래처럼 하면 되지 않을까요?
"$f(x)$을 얼마든지 원하는 만큼 $L$에 가깝게 만들 수 있다."
'가깝다'는 말을 절대값을 이용해서 바꿔보죠.
"임의의 양의 실수 $\epsilon$에 대해서 $|f(x)-L|<\epsilon$이 되도록 만들 수 있다."
이번에는 $x$가 무한대로 가는게 아니라 $a$ 근처로 가야 합니다. 이 부분을 설계해보죠. $x\rightarrow\infty$일 때 $1/x$의 극한값은 아래와 같이 썼습니다.
"임의의 양의 실수 $\epsilon$에 대해서 $0<1/x<\epsilon$인 실수 $x$가 존재한다."
비슷한 방식으로 표현하려면 아래와 같은 형태가 되어야 할 것 같습니다.
"임의의 양의 실수 $\epsilon$에 대해서 $|f(x)-L|<\epsilon$인 (뭐뭐)가 존재한다."
(뭐뭐)에는 뭘 쓰면 좋을까요? 아래 그림을 봅시다.
$|f(x)-L|<\epsilon$는 구간입니다. 아무리 작은 $\epsilon$에 대해서도 함수값이 $\left( L-\epsilon, L+\epsilon \right)$에 들어가게 하려면? 힌트는 '구간'에 있습니다. 우리가 바꿀 수 있는 것은 $x$밖에 없습니다. 그런데 $|f(x)-L|<\epsilon$여야 한다? 그렇다면 $|f(x)-L|<\epsilon$를 만족하는 $x$의 구간을 정할 수 있으면 됩니다. 말로 풀어쓰면 아래와 같습니다.
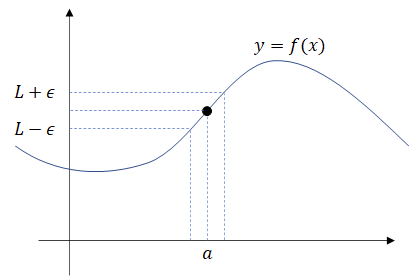
"임의의 양의 실수 $\epsilon$에 대해서, $|f(x)-L|<\epsilon$인 $x$의 구간이 존재한다."
구간을 $\delta$를 이용하여 써보죠.
"임의의 양의 실수 $\epsilon$에 대해서, $|f(x)-L|<\epsilon$인 $x$의 구간 $\left( a-\delta, a+\delta \right)$이 존재한다."
조금 더 수학적으로 표현하면 아래와 같습니다.
"임의의 양의 실수 $\epsilon$에 대해서, $|x-a|<\delta$인 모든 $x$가 $|f(x)-L|<\epsilon$를 만족하는 $\delta$가 존재한다."
살짝 표현이 난해해지기는 했지만, 유심히 쳐다보면 결국 같은 말임을 알 수 있습니다.
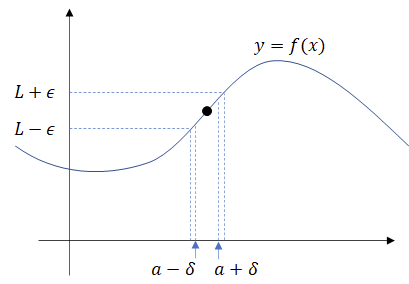
이러한 극한의 정의를, 정의에 들어간 $\epsilon$과 $\delta$를 이용하여 "엡실론 델타 논법"이라고 부릅니다. 너무 길군요. 입델이라고 부르기도 합니다. 아래는 나무위키의 엡실론 델타 논법을 캡쳐한 것입니다.
표현이 다소 다른 면이 있지만 결국 같은 얘기입니다.
대학교 1학년 때 미적분학 강의를 들었습니다. 고등학교 때까지 나름 수학 잘한다는 자부심이 있었는데, 강의 초장부터 문제는 하나도 안 풀고 처음보는 기호들과 논법들로 멘붕이었던 기억이 아직도 생생합니다. 그때는 도대체 왜 이렇게까지? 라고 생각했는데, 시간이 한참 지나고 나니 알겠더군요. 세상에 공짜는 없다는 것을.
무한의 개념을 이용하는 극한을 공짜로 쓸 수는 없습니다. 도대체 무한이 뭐지? 극한이 뭐지? 이렇게 막 써도 되나? 라는 고민을 19세기 수학자들이 본격적으로 하기 시작했고, 그 과정에서 나온 것이 엡실론-델타 논법입니다. 수학의 진정한 아름다움은 이런 엄밀함에서 오는 것 같습니다.
게으른