티스토리 뷰

우리는 $\mathbb{R}^2$를 다룰 때 마음 속에 아래와 같은 공간을 상정한다.

그런데 생각해보면 $\mathbb{R}^2$는 두 실수 $a$와 $b$에 대해서 $(a, b)$를 모은 것일 뿐, 여기에 길이나 각도를 준 적이 없다. 예를 들면 2차 다항식의 공간 $\mathbb{R}_2[x]$는 3차원 벡터공간인데, 이것의 기저를 $\{1, x, x^2\}$로 잡을 수는 있지만 $1$과 $x$가 직교하냐고 물으면 할 말이 없어진다.
익숙한 dot product는 아래와 같이 계산되는데,
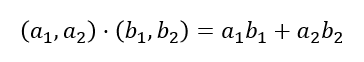
이것은 사실 아래의 과정을 축약한 것이다.

여기서 표준기저는 모두 길이가 1이고 서로 직교한다는 가정이 깔려있다. 하지만 꼭 그래야 할 이유는 없다. 예를 들어 나는 $(1, 0)$과 $(1, 1)$의 길이가 1이고 두 벡터가 직교한다고 말하고 싶다.
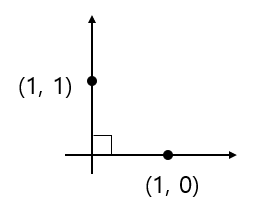
이제 임의의 벡터 $(x, y)$는 이 공간 어딘가에 있을텐데, 그것의 "좌표"는 더 이상 $(x, y)$가 아니다. $(x-y, y)$가 좌표가 된다.

이 벡터의 길이는 얼마일까? 표준기저와 다른 기저로 좌표축을 잡았을 뿐, 피타고라스 정리는 여전히 만족한다고 말하고 싶다.

이 공간은 분명히 표준내적(dot product)이 주어진 공간과 다르게 생겼다. 내적도 다른 기호를 써야 할 것 같으니, 앞으로는 아래와 같은 기호를 쓰자.

하지만 dot product와 동일하게 bilinearity는 만족했으면 좋겠다.
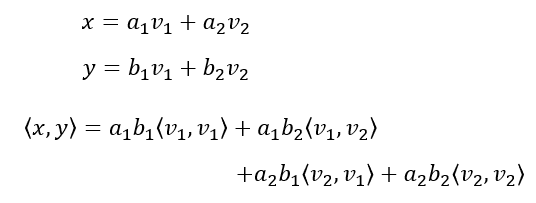
앞에서 잡았듯이 $(1, 0)$과 $(1, 1)$의 길이가 1이고 두 벡터가 직교한다고 하자. 2차원 벡터공간에서 직교하는 두 벡터는 기저가 된다. $v_1 = (1, 0)$, $v_2 = (1, 1)$이라고 두자. 이제 표준기저 두 벡터는 아래와 같으며,

이들의 크기와 사이각은 아래와 같다.

이제 아래와 같은 행렬을 생각해보자.
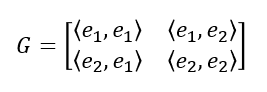
$\mathbb{R}^2$의 벡터는 여전히 $(a, b)$의 형태이다. 이제 두 벡터 $x=(a, b)$와 $y=(c, d)$의 내적은 아래와 같이 쓸 수 있다.

이 행렬 $G$를 Gram 행렬이라고 부른다. 앞의 예시에 대해 Gram 행렬 및 내적은 아래와 같다.
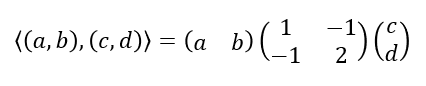
이번에는 Gram 행렬을 먼저 주고 직교하는 두 벡터를 찾아보자.
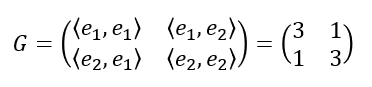
첫 번째 벡터는 아무렇게나 잡아도 된다. 첫 번째 벡터로 $v_1 = (1/3)e_1$을 잡자. 길이를 1로 맞추기 위해 1/3을 곱했다. 이제 $\Vert v_2 \Vert=1$이고 $\langle v_1, v_2 \rangle=0$인 $v_2$를 찾아보자. $v_2 = a_1e_1 + a_2e_2$로 두면
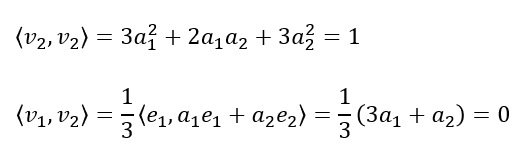
이 연립방정식을 풀어서 아래의 해를 얻을 수 있다.

그런데 사실 이 답은 Gram-Schmidt 과정으로도 구할 수 있다. 내적의 계산이 달라졌을 뿐 직교성을 이용하는 것은 변하지 않기 때문이다.

그런데 사실 이것보다 더 간단한 방법이 있다. Gram 행렬 $G$의 고유벡터 2개를 $v_1$, $v_2$라고 하자. $G$가 이미 대각행렬이라면 이미 직교하는 두 벡터를 찾은 것이므로 더 할 것이 없다. $G$가 대칭행렬이고 대각행렬이 아니라면 서로 다른 두 고유값과 각 고유값의 고유벡터가 하나 존재한다.

$G$가 대칭행렬이므로 이미 두 고유벡터는 직교한다. 하지만 이것은 표준내적에서 직교한다는 말이지, 내적이 Gram 행렬로 주어진 경우에도 직교하는지는 모른다. 이것을 확인해보자.

따라서 $G$의 두 고유벡터는 내적이 $G$로 정의되는 공간에서도 내적이다.
'mathe' 카테고리의 다른 글
| Field axioms and propositions (0) | 2025.10.03 |
|---|---|
| On Normal Distributions (0) | 2025.09.30 |
| 수학을 공부한다는 것 (0) | 2025.09.07 |
| 귀류법이란? (0) | 2025.09.07 |
| Rank-Nullity Theorem과 그 이면의 구조에 대하여 (0) | 2025.08.15 |
